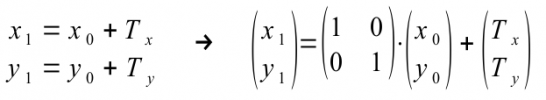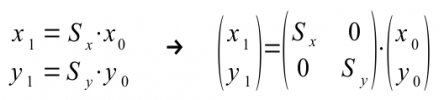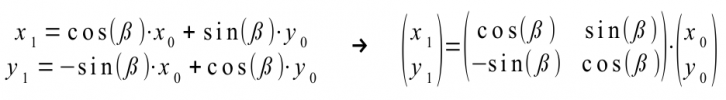Sidebar
Table of Contents
23.3.8 PaintMatrix
The PaintMatrix (gb.qt4) class represents a transformation matrix that is used, among other things, to execute affine mappings (translation, scaling, rotation).
Please note that all methods return the result matrix so that you can perform several transformations in one line of code by chaining method calls.
23.3.8.1 Creating a PaintMatrix
A new PaintMatrix can be generated with New PaintMatrix ([…]):
Dim hPaintMatrix As PaintMatrix hPaintMatrix = New PaintMatrix ([XX As Float,XY As Float,YX As Float,YY As Float,X0 As Float,Y0 As Float])
If the matrix elements are not specified, a unit matrix (identity) is created. You can also use the class like a static function that has a function value of type PaintMatrix:
Function PaintMatrix ([XX As Float,XY As Float,YX As Float,YY As Float,X0 As Float,Y0 As Float])
23.3.8.2 Methods
The PaintMatrix class only has methods.
| Method | Description |
|---|---|
| Function Translate ( TX As Float, TY As Float ) As PaintMatrix | Changes the PaintMatrix by the shifts TX and TY and returns the changed matrix. |
| Function Scale ( SX As Float, SY As Float ) As PaintMatrix | Changes the PaintMatrix with the scaling factors SX and SY and returns the changed matrix. |
| Function Rotate ( Angle As Float ) As PaintMatrix | Changes the PaintMatrix with the rotation angle (radians) and returns the changed matrix. |
| Function Reset ( ) As PaintMatrix | Resets the PaintMatrix to the identity matrix (unit matrix) and returns the changed matrix. |
| Function Multiply ( Matrix2 As PaintMatrix ) As PaintMatrix | Changes the PaintMatrix by multiplying it with the specified Matrix2 and returns the changed matrix. |
| Function Invert ( ) As PaintMatrix | Inverts the matrix and returns the modified matrix. If the matrix cannot be inverted, NULL is returned - which must be checked. |
| Function Copy ( ) As PaintMatrix | A copy of the current PaintMatrix is returned as an independent object. |
| Function Map ( Point As PointF ) As PointF | Applies the transformation to the given point (matrix-vector product) and returns the image vector. |
Table 23.3.8.2.1 : Methods of the PaintMatrix class
23.3.8.3 Notes
For a translation of a point P(x0|y0) → P'(x1|y1) in a Cartesian coordinate system (xy plane E), these transformation equations result for P(x0|y0) as the original point and with P'(x1|y1) as the image point. The equation on the right is the equivalent matrix notation for the description of a translation or displacement:
For all other points of the coordinate plane E, this equation also applies for a displacement by the displacement distance of Tx in the x-direction and Ty in the y-direction.
A scaling of the coordinate axes can be described with these two transformation equations, whereby the factors Sx and Sy are the scaling factors in both coordinate directions:
For the rotation of a point P(x0|y0) around the coordinate origin O(0|0) with a rotation angle ß, use the following transformation equations for the original and image point:
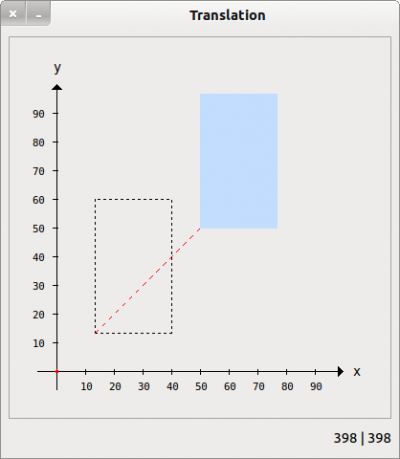
The following image shows the effects that can be achieved by translating a simple graphic:
Figure 23.3.8.3.1: Displacement of a rectangle