GAMBAS-BOOK 3.19.5

In this project by Tobias Boege, a Hilbert curve of any order is drawn - at least in theory. In practice, you can still see curves up to order 8 or 9 on a normal monitor.

Figure 23.3.5.8.1: Hilbert curve of 6th order

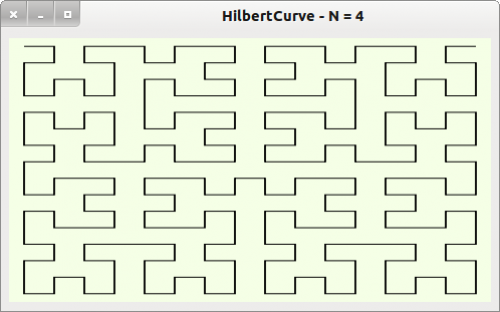
The programme starts with a Hilbert curve of order 4. You can change the order using the “+” and “-” buttons.

Figure 23.3.5.8.2: Start curve with N=4

The project source code is very short and shows the use of methods of the Paint class - in particular Paint.Scale() and Paint.Translate(). It shows how to write functions that are independent of the current Paint device, because the functions in the project can be used to draw on a DrawingArea as well as on a Picture without changing anything.

The source code is somewhat more difficult to read because the _HilbertCurve(…) procedure is partly programmed recursively and the source code is therefore very compact.

' Gambas class file
 
Private $iOrder As Integer = 4
Private $iX As Integer
Private $iY As Integer
 
Public Sub Form_Open()
  FMain.Center
  FMain.Height = (9 / 16) * FMain.Width
End
 
Public Sub Form_KeyPress()
  If Key.Code = Key["+"] Then
    Inc $iOrder
    dwgKurve.Refresh()
  Else If Key.Code = Key["-"] And If $iOrder > 0 Then
    Dec $iOrder
    dwgKurve.Refresh()
  Endif
 
End
 
Public Sub dwgKurve_Draw()
  $iX = 0
  $iY = 0
  Inc Application.Busy
    FMain.Title = "HilbertCurve - N = " & $iOrder 
    HilbertCurve($iOrder)
  Dec Application.Busy
End
 
Private Sub HilbertCurve(Order As Integer)
  With Paint.Device
    Paint.Scale(.W / 2 ^ Order, .H / 2 ^ Order)
    Paint.Translate(0.5, 0.5)
    Paint.LineWidth = 2 ^ Order / Min(.W, .H)
  End With
  _HilbertCurve(0, 1, Order)
  Paint.Stroke()
End
 
' Found in Warren, Henry S. Jr.: Hacker's Delight. 2nd ed. Addison-Wesley (2013), pp. 356ff.
' The routine is attributed to Voorhies, Douglas: Space-Filling Curves and a Measure of Coherence.
' Graphics Gems II, AP Professional (1991).
 
Private Sub _HilbertCurve(Direction As Integer, Rotation As Integer, Order As Integer)
  If Order = 0 Then Return
 
  Direction += Rotation
  _HilbertCurve(Direction, - Rotation, Order – 1) ' Recursion 1
  _HilbertStep(Direction)
 
  Direction -= Rotation
  _HilbertCurve(Direction, Rotation, Order - 1) ' Recursion 2
  _HilbertStep(Direction)
  _HilbertCurve(Direction, Rotation, Order - 1) ' Recursion 3
 
  Direction -= Rotation
  _HilbertStep(Direction)
  _HilbertCurve(Direction, - Rotation, Order - 1) ' Recursion 4
End
 
Private Sub _HilbertStep(Direction As Integer)
  Select Case Direction And 3
    Case 0
      Inc $iX
    Case 1
      Inc $iY
    Case 2
      Dec $iX
    Case 3
      Dec $iY
  End Select
  Paint.LineTo($iX, $iY)
End