Sidebar
Table of Contents
25.2.1 Class Clipper
The Clipper class (gb.clipper) implements clipping methods for polygons.
25.2.1.1 Methods
The Clipper class has these methods. Note the optional arguments, which are marked in blue:
| Method | Description |
|---|---|
| Clean( Polygons As Polygon[] [ , Distance As Float ] ) As Polygon[] | Removes corners that connect collinear sides (where the polygons involved have no real “visual” corners) or connect almost-collinear sides (in the sense that the sides are collinear, if the corner is shifted by at most Distance) or which are only at most Distance-far from an adjacent corner or which are only at most Distance-far from a semi-adjacent corner - together with the corner between them. |
| Difference( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[] | Calculates an array of polygons using the Difference method and returns it. The arguments of the Difference function are polygons in an array of polygons and a clip of the polygon data type. Fill is the polygon filling rule to be used. |
| ExclusiveOr( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[] | Calculates an array of polygons using the ExclusiveOr method and returns it. The arguments of the ExclusiveOr function are polygons in an array of polygons and a clip of the polygon data type. Fill is the polygon filling rule to be used. |
| Intersection ( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[] | Calculates an array of polygons using the Intersection method and returns it. The arguments of the intersection function are polygons in an array of polygons and a clip of the polygon data type. Fill is the polygon filling rule to be used. |
| Union ( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[] | Calculates an array of polygons using the Union method and returns it. The arguments of the union function are polygons in an array of polygons and a clip of the polygon data type. Fill is the polygon filling rule to be used. |
| Simplify ( Polygons As Polygon[] [ , Fill As Integer ] ) As Polygon[] | Removes all self-intersections of the polygons using the 'Union' operation based on the specified fill type. If two corners touch within a polygon, the polygon is divided into two polygons. Note the data type: Array of polygons |
Table 25.2.1.1.1 : Methods of the Clipper class
25.2.1.2 Constants
Each polygon or an arrangement of polygons must have a fill type when one of the following clipping methods is called: Difference, Union, Intersection or ExclusiveOr.
The constants for the polygon filling rules and the connection types are described here for the Clipper class.
| Constant | Value |
|---|---|
| Clipper.FillEvenOdd | 0 |
| Clipper.FillWinding | 1 |
| Clipper.FillNonZero | 1 |
| Clipper.FillPositive | 2 |
| Clipper.FillNegative | 3 |
| Constant | Value | Description |
|---|---|---|
| JoinSquare | 0 | This constant represents a “Square” connection type. |
| JoinRound | 1 | This constant represents a “Round” connection type. |
| JoinMiter | 2 | This constant represents a “Miter” connection type. |
Tables 25.2.1.2.1 : Constants of the Clipper class
25.2.1.3 Examples
You can find a project archive in the download area so that you can reproduce all the examples. You will also find the source texts used in the aforementioned chapter for the special polygons 'Rectangle' → Chapter 25.2.4 Classes Rect and RectF. For this reason, the complete example source texts are largely omitted. Only source code excerpts are presented and the results obtained are displayed. In principle, a picture is drawn, which is then displayed in a DrawArea. This is the only way to view the results when using the Clipper.Intersection, Clipper.Union, Clipper.ExclusiveOr or Clipper.Difference methods.
Example 1
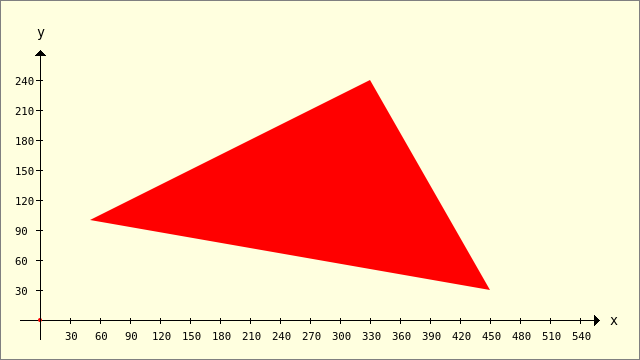
In the first example, a triangle is presented as a concave polygon. A polygon is concave if all connecting lines in the polygon always lie inside the polygon.
- First, a polygon with four corners is created and the coordinates of a selected point are read out and displayed in different ways.
- A point is then removed using the Clipper.Remove(point_index) method and the reduced polygon is assigned to another polygon pTriangel. Its points are read out and displayed, as is the area of the polygon.
- Finally, the polygon is displayed.
Public Sub ScriptPolygon1() Dim iIndex As Integer Dim pPolygon, pTriangle As New Polygon Dim Point As New PointF pPolygon.Add(50, 100) ' A pPolygon.Add(450, 30) ' B pPolygon.Add(330, 240) ' C pPolygon.Add(70, 123.4) ' D ' Read out the 4th corner point (index=3) and display the coordinates Dx and Dy Point = pPolygon[3] Print "Dx = "; Point.X Print "Dy = "; Point.Y Print "Dx = "; pPolygon[3].X ' Alternative Print "Dy = "; pPolygon[3].Y ' The point D(Index=3) is removed from the polygon pPolygon.Remove(3, 1) pTriangle = pPolygon ' Read out all corner points and display the coordinates of the triangle For iIndex = 0 To pTriangle.Max Point = pTriangle[iIndex] Print "Point"; iIndex + 1; ".x = "; Point.X; " Punkt"; iIndex + 1; ".y = "; Point.Y Next ' Calculate and display the area of the polygon Print "The triangle ABC has an area of "; Round(pTriangle.Area, 2); " Units of area!" GenerateNewPicture() SetPictureBorder() Paint.Begin(hPicture) Paint.Translate(xTranslate, yTranslate) Paint.Scale(xScale, yScale) ' +y ▲ Paint.AntiAlias = False DrawCoordinateSystem() ' +y ▲ Paint.Brush = Paint.Color(Color.Red) DrawPolygon(pTriangle, "f") Paint.AntiAlias = True Paint.End() End
This is the output in the IDE console:
Dx = 70 Dy = 123,4 Dx = 70 Dy = 123,4 Point1.x = 50 Point1.y = 100 Point2.x = 450 Point2.y = 30 Point3.x = 330 Point3.y = 240 The triangle ABC has an area of 37800 Units of area!
Figure 25.2.1.3.1: Polygon 'Triangle'
Example 2
Only a convex polygon is presented here:
Figure 25.2.1.3.2: Convex polygon
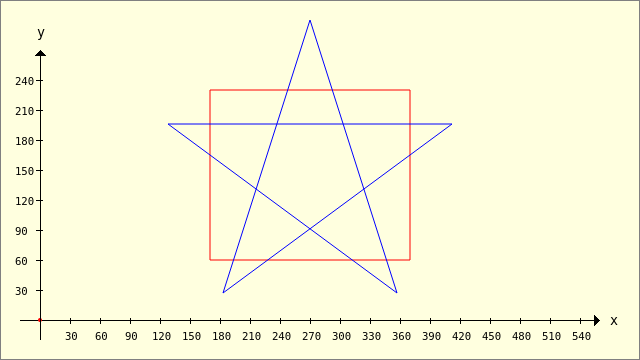
The same polygons are always used for the next four examples - a pentagram and a rectangle. Then the 4 methods
- Clipper.Intersection,
- Clipper.Union,
- Clipper.ExclusiveOr and
- Clipper.Difference
are used for four different fill rules, which essentially determine the result.
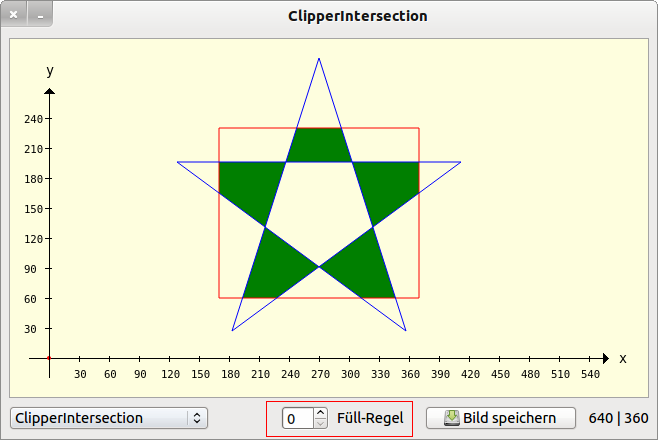
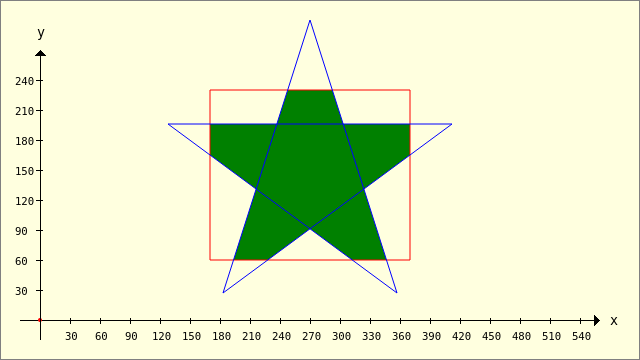
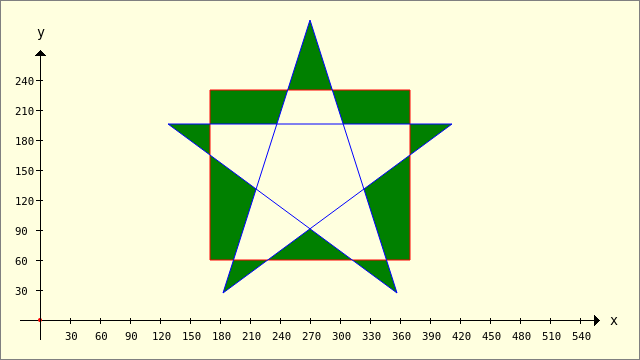
Example 3 - Clipper.Intersection(..)
Public Sub ScriptCIntersection() Dim pPentagramm, pRectangle, hP As New Polygon pPentagramm.Add(128, 196) pPentagramm.Add(412, 196) pPentagramm.Add(183, 27) pPentagramm.Add(270, 300) pPentagramm.Add(357, 27) pRectangle.Add(170, 230) pRectangle.Add(370, 230) pRectangle.Add(370, 60) pRectangle.Add(170, 60) GenerateNewPicture() SetPictureBorder() Paint.Begin(hPicture) Paint.Translate(xTranslate, yTranslate) Paint.Scale(xScale, yScale) ' +y ▲ Paint.AntiAlias = False DrawCoordinateSystem() ' +y ▲ Paint.Background = Color.DarkGreen For Each hP In Clipper.Intersection([pPentagramm], [pRectangle], sbFillRule.Value) ' 0..3 DrawPolygon(hP) Next Paint.Brush = Paint.Color(Color.Red) DrawPolygon(pRectangle, "s") Paint.Brush = Paint.Color(Color.Blue) DrawPolygon(pPentagramm, "s") Paint.End() End
Figure 25.2.1.3.3: Intersection - Filling rule selection (0..3)
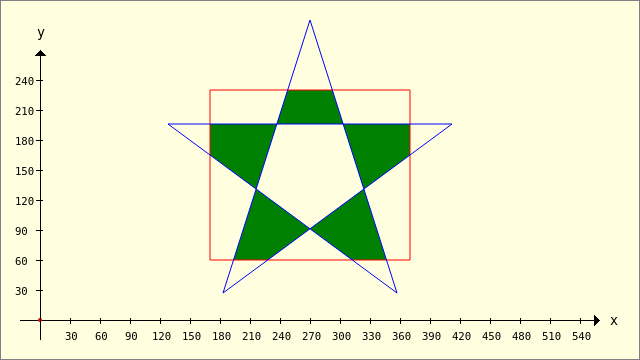
Figure 25.2.1.3.4: Intersection - Filling rule 0 (FillEvenOdd)
Figure 25.2.1.3.5: Intersection - Filling rule 1 (FillNonZero)
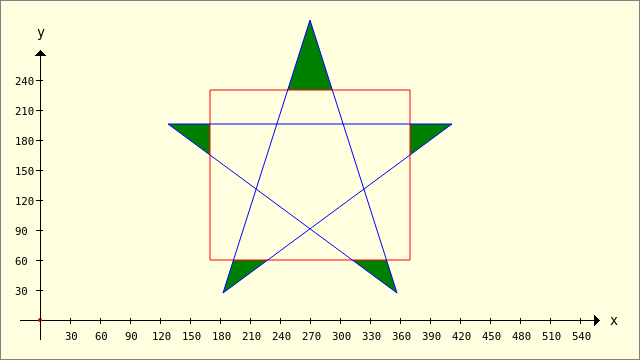
Example 4 - Clipper.Difference(..)
Figure 25.2.1.3.6: Difference - Filling rule 0 (FillEvenOdd)
Figure 25.2.1.3.7: Difference - Filling rule 2 (FillPositive)
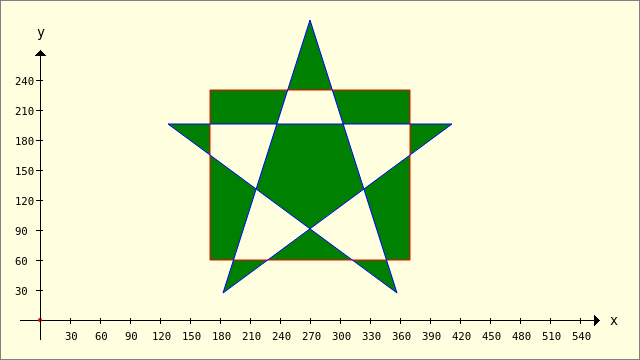
Example 5 - Clipper.ExclusiveOr(..)
Figure 25.2.1.3.8: ExclusiveOr - Filling rule 0 (FillEvenOdd)
Figure 25.2.1.3.9: ExclusiveOrder - Filling rule 1 and 3
Example 6.1 - Clipper.Union(..)
To illustrate the use of the Clipper.Union(..) method, only one image is shown because the images for filling rule 0, 1 and 3 are the same:
Figure 25.2.1.3.10: Union - fill rule 0 (FillEvenOdd)
Example 6.2 - Clipper.Union(..)
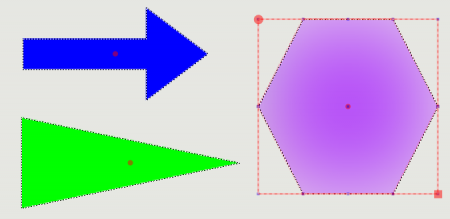
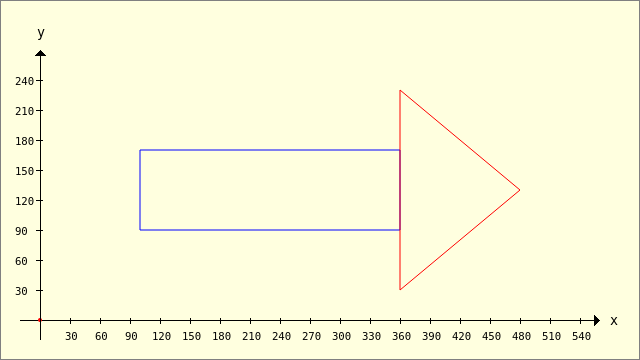
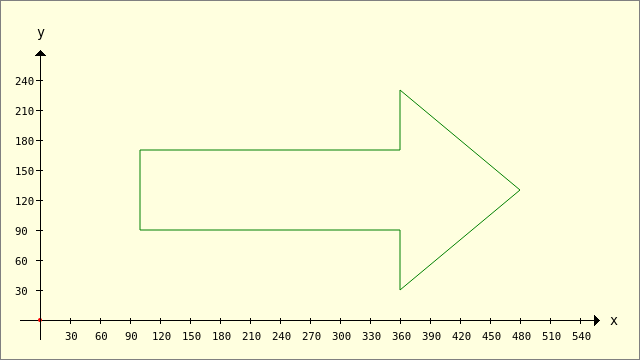
Using the Clipper.Union(..) method, you can, for example, combine shapes such as a rectangle and a triangle to form an arrow (union of polygons) and view them as a unit - as a geometric object.
Figure 25.2.1.3.11: Use: Shapes from the image editor of the Gambas IDE
Figure 25.2.1.3.12: A triangle and a rectangle
Figure 25.2.1.3.13: An arrow (envelope curve)
Use this source code to create the figure → 25.2.1.3.12, which also allows you to draw the (commented out) alternative:
Public Sub ScriptPolygon2() Dim iIndex As Integer Dim Point As New PointF Dim pPolygon, pTriangle, hP As New Polygon Dim aPolygon As Polygon[] pPolygon.Add(100, 170) ' A pPolygon.Add(360, 170) ' B pPolygon.Add(360, 90) ' C pPolygon.Add(100, 90) ' D pTriangle.Add(360, 230) ' P pTriangle.Add(480, 130) ' Q pTriangle.Add(360, 30) ' R aPolygon = Clipper.Union([pPolygon], [pTriangle], 0) GenerateNewPicture() SetPictureBorder() Paint.Begin(hPicture) Paint.Translate(xTranslate, yTranslate) Paint.Scale(xScale, yScale) ' +y ▲ Paint.AntiAlias = False DrawCoordinateSystem() ' +y ▲ Paint.Brush = Paint.Color(Color.DarkGreen) ' Rectangle and triangle Paint.Brush = Paint.Color(Color.Blue) DrawPolygon(pPolygon, "s") Paint.Brush = Paint.Color(Color.Red) DrawPolygon(pTriangle, "s") ' Arrow as a unit ' For Each hP In aPolygon ' DrawPolygon(hP, "s") ' Next Paint.End() End