Sidebar
Table of Contents
25.2.2 Class Polygon
The Polygon class (gb.clipper) represents a polygon. This chapter introduces the properties and methods of the Polygon class.
25.2.2.1 Properties
The Polygon class has these four properties:
| Property | Description |
|---|---|
| Count As Integer | Returns the number of corner points of a polygon. |
| Max As Integer | Returns the number of corner points of a polygon - reduced by 1. This corresponds to the largest index in the polygon array. |
| Area As Float | Returns the area of the polygon in area units. |
| Orientation As Boolean | Returns the orientation of a polygon (data type truth value). If the positive y-axis points downwards, true is returned for Orientation if the orientation of the polygon is clockwise. |
Table 25.2.2.1.1 : Properties of the Polygon class
25.2.2.2 Methods
All methods for the Polygon class are described here:
| Method | Description |
|---|---|
| Add( X As Float, Y As Float ) | Adds a new corner point to the polygon. |
| AddPoint( Point As Point ) | Adds a new corner point to the polygon. |
| Remove( Index As Integer [ , Count As Integer ] ) | Removes one or more points from the polygon. 'Index' is the index of the point to be removed. Count is the number of points to be removed from the 'Index' position. By default, one point is removed. |
| Reverse( ) | Inverts the existing orientation of the polygon. |
| Simplify( [ Fill As Integer ] ) As Polygon[ ] | Removes all self-intersections of the polygon using the union operation based on the specified fill type. If two corners touch within a polygon, the polygon is split into two polygons. |
| Clean( [ Distance As Float ] ) As Polygon | Removes corners that connect collinear sides (where the polygon has no true “visual” corner) or connect near-collinear sides (in the sense that the sides are collinear if the corner is moved by at most Distance) or that are only at most Distance away from an adjacent corner or that are only at most Distance away from a semi-adjacent corner - together with the corner between them. |
Table 25.2.2.2.1 : Methods of the Polygon class
Notes Simplify(..)
- This method is important for so-called non-simple polygons. These are polygons whose sides intersect and do not just touch at the corner points.
- A pentagram, for example, is a classic non-simple polygon. The fill rule then determines whether the pentagon that is created within the pentagram belongs to the “inside” of the polygon or the “outside”. When the polygon is constructed, the pentagon belongs to the interior first. The Simplify() method can then be called, if desired, with a suitable fill rule to remove the pentagon.
Notes Clean(..)
- Corners are semi-adjacent if there is exactly one other corner between them.
- The distance parameter is √2 by default, so that a corner is removed as soon as an adjacent or semi-adjacent corner exists whose x and y coordinates are no more than one unit of the coordinate system apart. If the corners are semi-adjacent, the corner between them is also removed.
- Distance is therefore a tolerance limit here. The Clean() method may make changes to the polygon in order to simplify it further. Distance also specifies how far points may be moved to allow greater simplification of the polygon.
25.2.2.3 Examples
This class can be created and used like an array:
Dim PolygonA, PolygonB As Polygon PolygonA = New Polygon '-- Polygon with 0 corners p.d. PolygonB = New Polygon(7) '-- Polygon with 7 corners
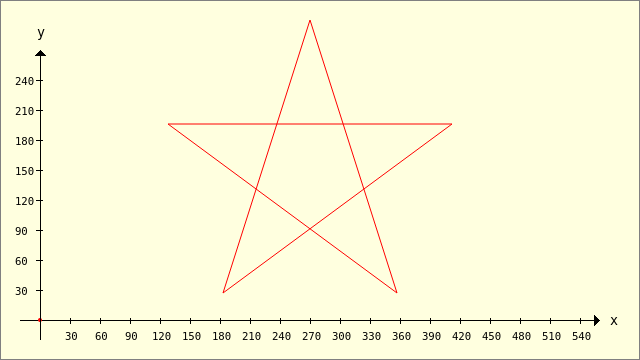
To define a polygon (pentagram) with 5 corner points (index 0..4) and read the number of corners, the orientation and the coordinates for all corner points from this polygon:
Public Sub ScriptPentagram() Dim iIndex As Integer Dim Point As PointF Dim pPolygon As New Polygon pPolygon.Add(128, 196) pPolygon.Add(412, 196) pPolygon.Add(183, 27) pPolygon.Add(270, 300) pPolygon.Add(357, 27) Print "Number of corner points = "; pPolygon.Count Print "Orientation = "; pPolygon.Orientation ' Read out all corner points and display the x,y coordinates of the corner points of the polygon For iIndex = 0 To pPolygon.Max Point = pPolygon[iIndex] Print "Point"; iIndex + 1; "(x) = "; Point.X; " Punkt"; iIndex + 1; "(y) = "; Point.Y Next GenerateNewPicture() SetPictureBorder() Paint.Begin(hPicture) Paint.Translate(xTranslate, yTranslate) Paint.Scale(xScale, yScale) ' +y ▲ Paint.AntiAlias = False DrawCoordinateSystem() ' +y ▲ Paint.Brush = Paint.Color(Color.Red) DrawPolygon(pPolygon, "s") '-- Argument 's' → draw lines, 'f' fill area Paint.End() End
Here you can see the output in the console of the IDE:
Number of corner points = 5 Orientation = False Punkt1(x) = 128 Punkt1(y) = 196 Punkt2(x) = 412 Punkt2(y) = 196 Punkt3(x) = 183 Punkt3(y) = 27 Punkt4(x) = 270 Punkt4(y) = 300 Punkt5(x) = 357 Punkt5(y) = 27
The images of the special polygon (→ pentagram) were drawn with all connecting lines on the one hand and as an image with the fill colour red on the other:
Figure 25.2.2.3.1: Pentagram (connecting lines)
Figure 25.2.2.3.2: Pentagram area