GAMBAS BOOK 3.19.1

If you want to give your restless informatics a clear direction and a goal, then you should apply algorithms with a recursive approach to sharply bend your brain in all directions. Recursion is a general procedure for splitting a task step-by-step into elementary solvable subtasks and applying the same algorithm to each subtask. In computer science, the Rekursion is an alternative to the control structure Repetition or Iteration/. The algorithms with a recursive approach are more elegant in their formulation and often shorter, but more difficult to understand in terms of content. This is also illustrated by the two mathematical examples presented, which first describe the mathematical task, then derive an inductively formulated function and finally present the algorithm for calculating the function values.

The calculation of the sum of natural numbers from 1 to i can be used as a function sum (i) = 1+2+….Define +i inductive like this:

• total (0) = 0 sum (i) = i + sum (i - 1) for i > 0

Calculation of the function values of sum (i):

PUBLIC FUNCTION summe(i AS Integer) AS Integer 
  IF i = 0 THEN 
     RETURN 0 
  ELSE 
    RETURN i + summe(k - 1) ' Recursive call with reduced argument! 
  ENDIF 
END ' summe(..) 

The calculation of the product of the natural numbers from 1 to k as a product (k) = 1 * 2 * 3 *… * k designates k-faculty and describes it with the symbol k! The function faculty (k) can thus be defined inductively:

• faculty (0) = 1 and faculty (1) = 1
• faculty (k) = k * faculty (k-1) for k > 1

Calculation of the functional values of faculty (k):

PUBLIC FUNCTION fakultaet(k AS Integer) AS Integer 
  IF k = 0 OR k = 1 THEN 
     RETURN 1 
  ELSE 
    RETURN k * fakultaet(k - 1) ' Recursive call with reduced argument! 
  ENDIF 
END

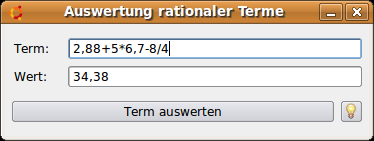
The task is quite simple: Calculation of the value of an expression with the following Input alphabet = {0.. 9, +, -, *, /, comma} taking into account the priority or ranking of the operations. The solution is based on the recursive descent method and provides, for example, for the expression 2,88+5*6,7-8/4/ as a value the rational number 34,38:

Figure 10.4.3.1: Evaluation for an expression

The complete source code is specified in the following section. Please note that the input characters of the entered expression are not checked and no error handling is built in to keep the source code as simple and legible as possible.

Source code:

' Gambas class file 
 
PUBLIC SUB Form_Open() 
  FMain.Center 
  FMain.Border = 1 
  txtTerm.SetFocus 
END 
 
PUBLIC SUB btnInfoAnzeigen_Click() 
  Balloon.Info("Input alphabet:" & Chr(10) & "0..9, + , - , * , / , Komma", LAST) 
END 
 
PUBLIC SUB txtTerm_Change() 
  txtWert.Clear 
END 
 
PUBLIC FUNCTION anfang(zeichenkette AS String, zeichen AS String) AS String 
  DIM position, anzahl AS Integer  
  position = InStr(zeichenkette, zeichen) 
  anzahl = position - 1 
  RETURN Mid$(zeichenkette, 1, anzahl)  
END 
 
PUBLIC FUNCTION copyab(zeichenkette AS String, i AS Integer) AS String 
  DIM anzahl AS Integer 
  anzahl = Len(zeichenkette) - i + 1 
  RETURN Mid$(zeichenkette, i, anzahl) 
END 
 
PUBLIC FUNCTION ende(zeichenkette AS String, zeichen AS String) AS String 
  DIM position, anzahl AS Integer 
  position = InStr(zeichenkette, zeichen) 
  anzahl = position + 1 
  RETURN copyab(zeichenkette, anzahl) 
END 
 
PUBLIC FUNCTION TermToReell(s AS String) AS Float 
  IF InStr(s, "+") > 0 THEN 
     RETURN TermToReell(anfang(s, "+")) + TermToReell(ende(s, "+")) 
  ELSE IF InStr(s, "-") > 0 THEN 
    RETURN TermToReell(anfang(s, "-")) - TermToReell(ende(s, "-")) 
  ELSE IF InStr(s, "/") > 0 THEN 
    RETURN TermToReell(anfang(s, "/")) / TermToReell(ende(s, "/"))
  ELSE IF InStr(s, "*") > 0 THEN 
    RETURN TermToReell(anfang(s, "*")) * TermToReell(ende(s, "*")) 
  ELSE 
    RETURN Val(s) 
  ENDIF 
END 
 
PUBLIC SUB btnTermAuswerten_Click() 
  txtWert.Text = Str(TermToReell(txtTerm.Text))  
END 

The TermToReell(expression) function, which is recursively called with constantly changing arguments, carries the main burden of calculating the value of the expression entered. For the simple expression 1+2*3-4/5, see how the value 6.2 has been calculated. To do this, it is also necessary to deal with the 3 functions used for processing character strings in order to find out what these functions do.

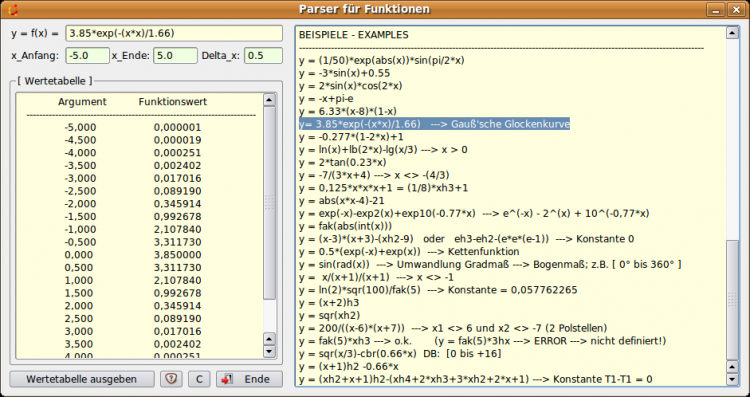
The algorithms presented belong to a subproject for a function parser, with which it was possible to calculate function values for a given f function. The complete project can be found in the download area together with the projects Term0 - from which the source code above originates - and Term0E. The Term0E project contains a character scanner and necessary error handling procedures.

The advantage of the developed and tested function saver is the definition of special functions such as faculty(k), which for example are not present in the component gb. eval.

Figure 10.4.3.2: Calculation of a value table with displayed help (foldable)