Sidebar
Table of Contents
11.5.2 Error prevention
This chapter is about pointing out possible sources of errors when programming. These hints should help you to convert the algorithms underlying the programs into Gambas source code as error-free as possible. The hints are varied and reflect the range of potential error sources.
11.5.2.1 Using experience
It has generally proved helpful to check the archives of the (English) mailing list for specific topics, in order to access the wealth of experience of other Gambas programmers or to be informed about news. Here's how to find what you're looking for:
Syntax: https://lists.gambas-basic.org/cgi-bin/search.cgi?q=suchliste_eintrag_getrennt_durch_+ Beispiel: https://lists.gambas-basic.org/cgi-bin/search.cgi?q=picturebox+clear
As far as new features in Gambas are concerned, keeping an eye on the mailing list and reading the 'Release Notes' is currently the only reliable way to be well informed, as the releases in the documentation are unfortunately not timely!
11.5.2.2 Gambas Release Notes - Changelog
You will save yourself grief, not only with older Gambas projects, if you carefully read the published changes as in http://gambaswiki.org/wiki/doc/release/3.12.2nh in new Gambas versions. Then you would be informed, for example, that the source code *** below is no longer allowed as of Gambas version 3.12.2! Before that it was possible to declare a global variable to use it this way:
Private hControl As Control '-- *** Public Sub Form_Open() For Each hControl In Me.Controls Print hControl.Name Next End
Correct as of Gambas version 3.12.2 is this source code:
Public Sub Form_Open()
Dim hControl As Control
For Each hControl In Me.Controls
Print hControl.Name
Next
End
Note that run variables in control structures must be local variables! Otherwise you will get an error message like 'Loop variable cannot be global in FMain.class:33'. This also means that you may have to adapt the source code in your older projects!
The following announcements in Gambas 3.12.2 only brought enhancements and additions to Gambas that you should know about - but errors do not result if you do not use these innovations. You are at an advantage, however, because you then understand source code that uses these extensions and additions.
- Local variables can now be declared anywhere in the function body.
- FOR and FOR EACH syntax now can declare their loop variables.
- String can now be accessed with the array syntax.
The following source code is correct:
[1] ' Gambas class file [2] [3] Public Sub btnTest_Click() [4] [5] Dim sString As String [6] [7] sString = "Gambas" [8] Print "sString = "; [9] For iCount As Integer = 0 To sString.Len – 1 [10] Print sString[iCount]; [11] Next [12] Print [13] [14] Dim aString As String[] [15] [16] aString = ["G", "a", "m", "b", "a", "s"] [17] Print "aString = ["; [18] For iCount As Integer = 0 To aString.Count – 1 [19] Print aString[iCount]; [20] Next [21] Print "]" [22] [23] Dim i As Integer = 1 [24] [25] While i < 10 [26] i = i * 2 [27] Wend ' i ist 16 = 2^4 [28] [29] Dim j As Integer = i ^ 2 ' 16^2 = 256 [30] Print j [31] [32] End
This is the output: in the console of the IDE:
sString = Gambas aString = [Gambas] 256
Comment
- The declarations in lines 5, 14, 23 and 29 are allowed. This does not change the default: “A variable can only be used after it has been declared”!
- In lines 9 and 18, the local variables iCount are declared within the control structure. The use of the same identifiers for the so-called run variables is permitted.
- The note “Strings can now be accessed with array syntax.” must be put into perspective. Obviously, only the possibility of accessing the individual characters via the index with String[index] is meant. However, there is no class behind a native string and therefore no methods like String.Count exist. It can be assumed that the array access to strings is a hack in the compiler that allows this syntax and handles it specially.
- In line 29, the variable j is actually initialised with a value that depends on the calculation steps preceding its declaration in lines 25 to 27. The variable j is only available below its declaration.
11.5.2.3 Gambas conventions
A thorough knowledge of the following Gambas conventions will allow you to better understand an (unknown) source code and prevent errors in your own source codes. Thus:
If a (boolean) function (dialogue) is named after an action (Connect, Close, …), then it returns `False` on success and `True` on failure.If the method (or property) is named after an attribute (IsEmpty, IsVector, …), then the return value is according to the name.
Example 1
A prime example is the method Dialog.Open(). This method is named after an action (Open) and returns False if a file was successfully selected to be opened:
If Dialog.Open() Then Return '-- Sie können jetzt die Eigenschaft Dialog.Path verwenden ...
If the return value of Dialog.Open() is True - which is the error case (!) - then the dialogue should be cancelled with Return. Otherwise you can use the Dialog.Path property.
Example 2
Private Function IsVector(sInput As String) As Boolean Dim sSubject, sPattern As String sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Not Match sPattern Then Return False ' Fehler Return True ' Erfolg End
This function - named after the attribute IsVector - returns `True` for success and `False` for failure, as expected.
You do not have to judge these above-mentioned conventions according to logic or sense. You only have to know and observe them! Thus they are part of the Gambas programming paradigm. If you use your own conventions in your projects, you can do so. Only then it is difficult for other programmers to understand or use the source code. Errors are then - in the true sense of the word - pre-programmed.
The conversions of truth values `True and `False` into numerical values also belong to this group of topics:
Dim bComparisonA, bComparisonB As Boolean bComparisonA = (8 > 5) bComparisonB = (Pi() = 355 / 113) Print CBoolean(bComparisonA) Print CString(CInt(bComparisonA)) Print CBoolean(bComparisonB) Print CString(CInt(bComparisonB))
These are the output:s in the console of the IDE:
True -1 False 0
11.5.2.4 Numerics - Number comparisons, rounding errors and overflow
See this page: http://gambaswiki.org/wiki/cat/float for interesting details on floating point numbers.
Example 1:Number comparisons of the kind If a = b Then … should be avoided. It is better to use an epsilon environment after a transformation If (a-b) = 0 Then … use an epsilon environment |a - b| smaller ε with ε ∈ ℝ and ε greater than 0:
Public fEpsilon As Float fEpsilon = 0.0001 If Abs(a-b) < fEpsilon Then ...
The rationale for this approach is that the computer numbers are discrete, rounding errors (can) occur in the calculations and these add up.
Example 2 shows different results for the same calculation with differently rounded results:
~ $ gbx3 -e "tan(rad(45))-1" ' Erwartet wird Null Output: -1,11022302462516E-16 ~ $ gbx3 -e "round(tan(rad(45))-1,-1)" Output: 0 ~ $ gbx3 -e "round(tan(rad(45))-1,-15)" Output: 0 ~ $ gbx3 -e "round(tan(rad(45))-1,-16)" Output: -1E-16
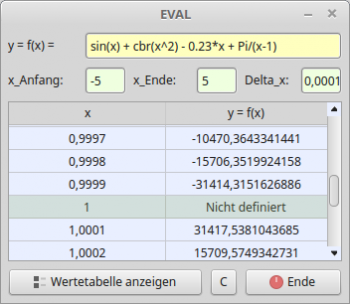
Example 3: When calculating the value table of the function f(x) = sin(x) + cbr(x^2) - 0.23*x + Pi/(x-1) in the interval -5 ≤ x ≤ +5, there were already errors at small step sizes ∆x in the form that it did not produce the expected text 'Not defined' for the pole position xp = 1. This text is output: if no function value can be calculated for a certain argument:
∆x x f(x) ------------------------------------------------- 0,1 1 -2,82969510081138E+16 0,01 0,99999999999994 -5,09854973119151E+13 0,001 1 +4,7161585013523E+15 ------------------------------------------------- Tabelle 1
There is a significant improvement if the step size ∆x is chosen as a power of two with 2^k and k ∈ {-1,-2,…,-9,-10,-11}:
∆x x f(x) ------------------------------------------- 1/2 1 Not defined 1/4 1 Not defined 1/8 1 Not defined ... 1/512 1 Not defined ... 1/4096 1 Not defined ------------------------------------------- Tabelle 2
You can derive the improvement from the IEEE-754 standard [https://de.wikipedia.org/wiki/IEEE_754] for the representation of floating-point numbers. According to this, you can represent any real number z as.
z = σ⋅m⋅2^e
where σ is the sign +1 or -1, m is the so-called mantissa and e is the exponent. A number of the float type is stored as a triple (σ,m,e). Since only 64 bits are available, these 64 bits must be divided among the sign σ, mantissa m and exponent e. According to the IEEE-754 standard, the specification is: σ needs exactly 1 bit, m gets 52 bits and e the remaining 11. You realise that numbers z can be stored exactly with ±2^e as long as the exponent remains in its 11 bits, i.e. between -1022 and 1023. Furthermore, the addition of this z to a number of the float type is exact if the exponents are close enough to each other.
Conclusion: Powers of two can be stored correctly. This makes them more suitable for step sizes than, say, 1/10, whose storage alone inherently causes rounding errors, as shown in the following example number z = 0.1; data type single (32-bit representation):
Zahl: 0.1 Single: 0.100000001490116119384765625 Fehler: 1.490116119384765625E-9 Binär: 00111101110011001100110011001101 Hex: &H3DCCCCCD Zahl: 0.0001220703125 = 1/8192 = 2^(-13) Single: 0.0001220703125 Fehler: 0 Binär: 00111001000000000000000000000000 Hex: &H39000000
A further improvement is achieved by implementing the following considerations. In the function to calculate the function value, the first version said:
Repeat
' ...
x += Me.DeltaX
Until x >= Me.EndX
This adds up rounding errors in the argument x, because with x += Me.DeltaX every single addition is error-prone. This is exactly what leads to the values in Table 1.
It is better to recalculate the argument x like this in each iteration:
i = 0
Repeat
' ...
Inc i
x = Me.StartX + i * Me.DeltaX
Until x >= Me.EndX
The results obtained when calculating the function value for different step sizes ∆x are convincing:
∆x x f(x) ------------------------------------------- 0,1 1 Nicht definiert 0,01 1 Nicht definiert 0,001 1 Nicht definiert 0,0001 1 Nicht definiert ------------------------------------------- Tabelle 3
Figure 11.5.2.4.1: Table of values for f(x)
11.5.2.5 Intercept overflow
Public Const MinFloat As Float = -8.98846567431105E+307 Public Const MaxFloat As Float = +8.98846567431105E+307 With aValuePair grdData[i,0].Text = Str(.X) grdData[i,1].Text = If(.Valid,If((.Y < MinFloat) Or (.Y > MaxFloat),"Überlauf",Str(.Y)), "nicht definiert") End With
If you use the format function Format$(…) for the output:, you must dispense with the exponential representation. But this can lead to nonsensical output: values, because an overflow is then not shown to you. If you receive an overflow error [http://gambaswiki.org/wiki/error/overflow] in a programme with many calculations, this means: The interpreter has determined that the result of a calculation is too large. The JIT compiler also performs overflow checks.
Example 1: This error occurs when a number fFL of type Float or Long is converted to a number of type Single, but the number fFL is too large:
~ $ gbx3 -e 'CStr(CSingle(2 ^ 500))' Output: Overflow
Example 2: This error occurs when the arithmetic with dates produces a value with more than 32 bits:
~ $ gbx3 -e 'CStr(DateDiff(CFloat(2 ^ 50), CFloat(1), gb.Second))' Output: Overflow
11.5.2.6 Valid data
As a programme developer, you should ensure that only valid data is processed in your programmes to prevent runtime errors. The data to be processed comes from very different data sources. They are
either read in via (external) data memories or made available in real time by sensors via suitable interfaces or arise as (temporary) data - for example as the result of calculations - at the runtime of the programme or are entered from suitable control elements such as TextBox or ValueBox via a keyboard or selected with the mouse, for example from a spin box. They are then converted into the required data type and finally validated.
In chapter '6.6.2 Valid Data' many ways to valid data are described in detail.
11.5.2.7 Automatic type conversion
Would you have expected the results in the console output: in the IDE to be like this:
Dim s As String = "44"
Print "Typ = "; TypeOf(3 * s); " ▸ "; 3 * s
Print "Typ = "; TypeOf(True); " ▸ "; True
Print "Typ = "; TypeOf("10"); " ▸ "; "10"
Print "Typ = "; TypeOf(Pi(2)); " ▸ "; Pi(2)
Print "Typ = "; TypeOf(Now()); " ▸ "; Now()
Print "Typ = "; TypeOf(Date(Now())); " ▸ "; Format$(Date(Now()), "dd.mm.yyyy")
Print "Typ = "; TypeOf(Day(Now())); " ▸ "; Day(Now())
Print "Typ = "; TypeOf(CString(3 * CInteger(s))); " ▸ "; CString(3 * CInteger(s))
Output: in the console of the IDE:
Typ = 7 ▸ 132 ' Float Typ = 1 ▸ True ' Boolean Typ = 9 ▸ 10 ' String Typ = 7 ▸ 6,28318530717959 ' Float Typ = 8 ▸ 01.04.2019 20:03:03 ' Date Typ = 8 ▸ 01.04.2019 ' Float Typ = 4 ▸ 1 ' Integer Typ = 9 ▸ 132 ' String
The remarkable thing about all the output: is that they are obviously all (automatic) conversions to the string data type, because the Print statement only output:s strings! Are you surprised that even a multiplication of an integer number with a string containing an integer number is accepted - but the product 3*s is of type float?
In similar conversions as with x and y as floating point numbers (data type Float), three conversions from Float to String take place:
Dim x, y As Float
x = Round(Pi(3), -4)
y = 10.0
Print x & " - " & y & " = " & (x - y)
Print Subst$("&1 - &2 = &3", x, y, x - y) ***
Output: 9.4248 - 10 = -0.5752
The output: *** gives the same result, but is preferable to the print statement above. This has the advantage that such string templates as “&1 - &2 = &3” are easier to translate into other languages, which does not always work well with multiple concatenation of strings. It is also easy to see that a difference of 2 operands is to be output:. A small hint - not only on the side: The print instruction does not use CString() internally, but the method Str$(). In the terminal, you will therefore always see the locale-afflicted output: of data!
11.5.2.8 Explicit type conversion
For explicit type conversions, aspects of localisation (locale) must be taken into account. According to Wikipedia (https://de.wikipedia.org/wiki/Locale), “The locale is a set of settings that contains the locale parameters (location parameters) for computer programs. These primarily include the user interface language, country and settings for character set, keyboard layout, number, currency, date and time formats. A set of settings is usually uniquely identified with a code that usually includes language and country.” Gambas uses the (system) locale of the standard library (GLib).
This comes into play when validating dates or numeric values, converting between dates or numeric values and strings. There are two levels of conversion functions:
- The lower level contains the functions such as CInt(), CFloat() or CString() - described in the documentation at http://gambaswiki.org/wiki/cat/conv. The lower level functions do not take the current locale into account. They should be used if, for example, you want to save a number as a string in a file and later read it back in as a number.
- The upper level consists of the functions Val$(), Str$() and Format$(). These functions take into account the current locale. For example, a number is formatted with the correct decimal separator, or the components of a date are formatted according to the order and separators commonly used in the current locale. This level is intended for displaying data to the user.
===== 11.5.2.8.1 Validating numeric values - full stop or comma - that is the question here =====.
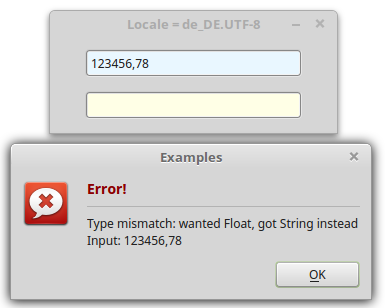
The answer will only matter if you allow the user to enter and display real numbers according to their locale, for example in a text box. If, however, you want the English number format to be used consistently with a dot as the decimal separator, use the functions CFloat(Expression AS Variant) for converting the read-in string into a floating-point number of the data type Float and the function CString(Expression AS Variant) for converting the floating-point number into a string. Note:
Internally, Gambas always works with the English number format for floating point numbers. In a German locale, the decimal separator is a comma and the dot is the thousands separator when dividing numbers into groups of digits (groups of three). In an English locale, the decimal separator is a point and the comma is the thousands separator when dividing numbers into groups of digits (groups of three).
Case 1 - English number format
A floating point number (data type Float) is to be entered via a text box in English number format and the result of internal calculations is to be displayed in another text box in the same number format. The current locale is not taken into account! The solution is shown in the following source code:
Public Sub TextBox1_Activate() Dim fValue, fResult As Float Dim sMessage As String Try fValue = CFloat(TextBox1.Text) If Error Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= Error.Text & "<br>" sMessage &= "Input: " & TextBox1.Text Message.Error(sMessage) Else fResult = Round(fValue * Pi(3.66), -3) TextBox2.Text = CString(fResult) Endif End
Figure 11.5.2.8.1: English number format - independent of the locale
Figure 11.5.2.8.2: English number format - independent of locale
Case 2 - Local number format
In contrast to the 1st case, the current locale is to be taken into account! For this reason, the source text uses other functions for validation and conversion (string ↔ number and number ↔ string):
Public Sub TextBox1_Activate() Dim fValue, fResult As Float Dim sMessage As String If Not IsFloat(TextBox1.Text) Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= "No floating-point number - related to the current locale." Message.Error(sMessage) Else fValue = Val(TextBox1.Text) fResult = Round(fValue * Pi(3.66), -3) TextBox2.Text = Str$(fResult) Endif End
Comment
- Note that the datatype functions - unlike CFloat(), for example - never throw an error, which therefore makes a construct of Try and If Error dispensable.
- Alternatively, you can also use the format function Format$() for Str$().
- In German, “123.456” is also considered a floating point number, but “123.45” is not, because the thousands separator is not recognised as such due to the missing group of three.
- The check with IsFloat(…) before the conversion with Val(…) is necessary, as you can see in the following example:
$ LC_NUMERIC=de_DE.utf8 gbx3 -e 'Str(Val("1.2"))'
Output: 01.02.2019 00:00:00
Digression
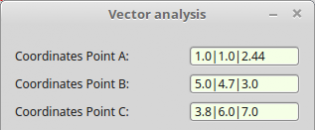
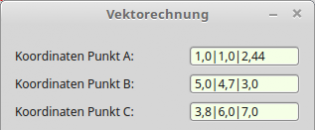
For a vector calculation project, special default values should be entered into a text box at the start of the programme, depending on the current locale:
Figure 11.5.2.8.3: Default values depending on the current locale
The implementation is simple, because the decimal separator used in the current locale is determined and taken into account:
Public Sub Form_Open() ... Init() ... End Private Sub Init() If Left$(Format$(0, ".0")) = "," Then txbInputA.Text = "1,0|1,0|2,44" txbInputB.Text = "5,0|4,7|3,0" txbInputC.Text = "3,8|6,0|7,0" Else txbInputA.Text = "1.0|1.0|2.44" txbInputB.Text = "5.0|4.7|3.0" txbInputC.Text = "3.8|6.0|7.0" Endif End
To prevent input errors in the text boxes, you can specify an input alphabet for the inputs and use the locale-consciously. In the specified case, all three TextBoxes are combined into one group:
Private Sub CheckInput(sAllowed As String) ' Idee: Charles Guerin Select Case Key.Code Case Key.Left, Key.Right, Key.BackSpace, Key.Delete, Key.End, Key.Home, Key.Enter, Key.Return Return Default If Key.Text And If InStr(sAllowed, Key.Text) Then Return Endif End Select Stop Event End Public Sub TBGroup_KeyPress() ' Gilt für die *TextBox-Gruppe* TBGroup! If Left$(Format$(0, ".0")) = "," Then CheckInput("+-,|0123456789") Else CheckInput("+-.|0123456789") Endif End
However, you cannot do without validating the input. This is no problem with the following function:
Private Function IsVector(sInput As String) As Boolean Dim sSubject, sPattern As String sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Not Match sPattern Then Return False Return True End
11.5.2.8.2 Date and floating point numbers
The function value of the Now() function represents the current date. This date value is mapped internally in Gambas to a floating point number of the float data type. The float representation of a date is not fully documented. There is a reference to it in the documentation for the function Frac(…) in http://gambaswiki.org/wiki/lang/frac. The date is described in the float by the integer part and the time by the fractional part:
Print Now() Print "Datum Σ: "; CFloat(Now()) Print "Datum: "; CInt(Now()) Print "Zeit: "; Round(Frac(Now()), -8)
04.04.2019 19:19:10 Datum Σ: 2490682,72164661 Datum: 2490682 Zeit: 0,72164661
The integer part represents the number of days since a certain point in time, which can be called the beginning of the “Gambas calendar”. Remember that 1/1/1970 is considered the beginning of the UNIX calendar because conventional timestamps on UNIX-type systems count the seconds since that date? The Gambas calendar, on the other hand, starts with the year 4801 BC as the following output: shows:
$ gbx3 -e 'CString(CDate(1))' Output: 01/01/-4801
However, in the Gambas documentation [http://gambaswiki.org/wiki/lang/time] there is a statement that the Gregorian calendar does not know year 0. In Gambas, the year 0 is used to indicate dates that have only a time part.
Now to the time: The fractional part is a floating point number of the data type float in the half-open interval [0,1). It describes the time of day as a part of the 24 hours of a day. For example, a time fraction of 0.5 corresponds to a time of day of 12 o'clock sharp:
$ gbx3 -e 'CString(CDate(0.5))' Output: 12:00:00
It is unknown whether one has to pay attention to the (float) rounding errors that occur with dates. On the one hand, one cannot represent a time like 8:00 exactly because there is no exact binary representation for 1/3 (of a day). On the other hand, the float approximation is accurate far beyond nanoseconds.
$ gbx3 -e 'CString(CDate(1/3))' 08:00:00 Print CString(CFloat(Time(8, 0, 0))) Output: 0.33333333333333
Thus, mapping a date to a floating point number of the float data type is a clever idea. If you store a date in the future, you can also take this gambas-specific date format. Note that these floating point numbers are used implicitly in Gambas when performing operations on dates.
11.5.2.8.3 UTC and GMT
UTC (Universal Time Coordinated) is the basis for calculating local times around the world. Note that
Internally, Gambas always works with the English number format for floating point numbers. In a German locale, the decimal separator is a comma and the dot is the thousands separator when dividing numbers into groups of digits (groups of three). In an English locale, the decimal separator is a point and the comma is the thousands separator when dividing numbers into groups of digits (groups of three).
Case 1 - English number format
A floating point number (data type Float) is to be entered via a text box in English number format and the result of internal calculations is to be displayed in another text box in the same number format. The current locale is not taken into account! The solution is shown in the following source code:
Public Sub TextBox1_Activate() Dim fValue, fResult As Float Dim sMessage As String Try fValue = CFloat(TextBox1.Text) If Error Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= Error.Text & "<br>" sMessage &= "Input: " & TextBox1.Text Message.Error(sMessage) Else fResult = Round(fValue * Pi(3.66), -3) TextBox2.Text = CString(fResult) Endif End
Figure 11.5.2.8.1: English number format - independent of the locale
Figure 11.5.2.8.2: English number format - independent of locale
Case 2 - Local number format
In contrast to the 1st case, the current locale is to be taken into account! For this reason, the source text uses other functions for validation and conversion (string ↔ number and number ↔ string):
Public Sub TextBox1_Activate() Dim fValue, fResult As Float Dim sMessage As String If Not IsFloat(TextBox1.Text) Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= "No floating-point number - related to the current locale." Message.Error(sMessage) Else fValue = Val(TextBox1.Text) fResult = Round(fValue * Pi(3.66), -3) TextBox2.Text = Str$(fResult) Endif End
Comment
- Note that the datatype functions - unlike CFloat(), for example - never throw an error, which therefore makes a construct of Try and If Error dispensable.
- Alternatively, you can also use the format function Format$() for Str$().
- In German, “123.456” is also considered a floating point number, but “123.45” is not, because the thousands separator is not recognised as such due to the missing group of three.
- The check with IsFloat(…) before the conversion with Val(…) is necessary, as you can see in the following example:
$ LC_NUMERIC=de_DE.utf8 gbx3 -e 'Str(Val("1.2"))'
Output: 01.02.2019 00:00:00
Digression
For a vector calculation project, special default values should be entered into a text box at the start of the programme, depending on the current locale:
Figure 11.5.2.8.3: Default values depending on the current locale
The implementation is simple, because the decimal separator used in the current locale is determined and taken into account:
Public Sub Form_Open() ... Init() ... End Private Sub Init() If Left$(Format$(0, ".0")) = "," Then txbInputA.Text = "1,0|1,0|2,44" txbInputB.Text = "5,0|4,7|3,0" txbInputC.Text = "3,8|6,0|7,0" Else txbInputA.Text = "1.0|1.0|2.44" txbInputB.Text = "5.0|4.7|3.0" txbInputC.Text = "3.8|6.0|7.0" Endif End
To prevent input errors in the text boxes, you can specify an input alphabet for the inputs and use the locale-consciously. In the specified case, all three TextBoxes are combined into one group:
Private Sub CheckInput(sAllowed As String) ' Idee: Charles Guerin Select Case Key.Code Case Key.Left, Key.Right, Key.BackSpace, Key.Delete, Key.End, Key.Home, Key.Enter, Key.Return Return Default If Key.Text And If InStr(sAllowed, Key.Text) Then Return Endif End Select Stop Event End Public Sub TBGroup_KeyPress() ' Gilt für die *TextBox-Gruppe* TBGroup! If Left$(Format$(0, ".0")) = "," Then CheckInput("+-,|0123456789") Else CheckInput("+-.|0123456789") Endif End
However, you cannot do without validating the input. This is no problem with the following function:
Private Function IsVector(sInput As String) As Boolean Dim sSubject, sPattern As String sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Not Match sPattern Then Return False Return True End
11.5.2.8.2 Date and floating point numbers
The function value of the Now() function represents the current date. This date value is mapped internally in Gambas to a floating point number of the float data type. The float representation of a date is not fully documented. There is a reference to it in the documentation for the function Frac(…) in http://gambaswiki.org/wiki/lang/frac. The date is described in the float by the integer part and the time by the fractional part:
Print Now() Print "Date Σ: "; CFloat(Now()) Print "Date: "; CInt(Now()) Print "Time: "; Round(Frac(Now()), -8)
04.04.2019 19:19:10 Date Σ: 2490682,72164661 Date: 2490682 Time: 0,72164661
The integer part represents the number of days since a certain point in time, which can be called the beginning of the “Gambas calendar”. Remember that 1/1/1970 is considered the beginning of the UNIX calendar because conventional timestamps on UNIX-type systems count the seconds since that date? The Gambas calendar, on the other hand, starts with the year 4801 BC as the following output: shows:
$ gbx3 -e 'CString(CDate(1))' Output: 01/01/-4801
However, in the Gambas documentation [http://gambaswiki.org/wiki/lang/time] there is a statement that the Gregorian calendar does not know year 0. In Gambas, the year 0 is used to indicate dates that have only a time part.
Now to the time: The fractional part is a floating point number of the data type float in the half-open interval [0,1). It describes the time of day as a part of the 24 hours of a day. For example, a time fraction of 0.5 corresponds to a time of day of 12 o'clock sharp:
$ gbx3 -e 'CString(CDate(0.5))' Output: 12:00:00
It is unknown whether one has to pay attention to the (float) rounding errors that occur with dates. On the one hand, one cannot represent a time like 8:00 exactly because there is no exact binary representation for 1/3 (of a day). On the other hand, the float approximation is accurate far beyond nanoseconds.
$ gbx3 -e 'CString(CDate(1/3))' 08:00:00 Print CString(CFloat(Time(8, 0, 0))) Output: 0.33333333333333
Thus, mapping a date to a floating point number of the float data type is a clever idea. If you store a date in the future, you can also take this gambas-specific date format. Note that these floating point numbers are used implicitly in Gambas when performing operations on dates.
11.5.2.8.3 UTC and GMT
UTC (Universal Time Coordinated) is the basis for calculating local times around the world. Note:
- Coordinated Universal Time (UTC) is a reference time for calculating local times in different time zones around the world.
11.5.2.8.4 Programme Test in a Changed Locale
If you translate your projects into other languages, then you should also test these projects in an adapted test environment in order to detect and eliminate possible errors. You can use entries in the project properties to work in a modified locale for each project, which must be installed on the system. Use the command `locale` to get an overview of the current locale on your system:
$ locale LANG=de_DE.UTF-8 ... LC_NUMERIC=de_DE.UTF-8 LC_TIME=de_DE.UTF-8 ... LC_IDENTIFICATION=de_DE.UTF-8 LC_ALL=
In the Gambas IDE, use the entry Menu> ?> `System Information …` with similar results. Then use Menu> Project> Properties> Environment to enter the following environment variable: Variable: LC_ALL with the value: en_GB.utf8 if you are working in a German locale and change to the English locale. After the successful test you can delete the variable.
Alternatively, start Gambas with this configuration: `$ LC_ALL=en_GB.utf8 gambas3` in the specified locale. The change is only temporary. It does not permanently change anything in the configuration files or the projects. A finely granulated setting, for example, only for numbers and times, can be achieved with: `$ LC_NUMERIC=en_GB.utf8 LC_TIME=en_GB.utf8 gambas3`.
11.5.2.8.5 Working with dates
The following section is a supplement to the chapters `9.10 Conversion functions` and `9.3 Date and time functions`. The focus is on hints for working with dates with regard to possible sources of error. The following stipulation applies: When writing of the date, then - depending on the context - either the complete date, the calendar day or only the time is meant. Date components are seconds, minutes and hours as well as day, month and year. If you are working with dates, this requires special attention if, in addition to the time zones (locales) - there are several for Europe alone - time changes such as daylight saving time come into play and have to be taken into account. In order to prevent errors, some hints on working with dates are then given, which are then supported with selected examples:
In order to present unambiguous dates, you should specify which time zone is meant and therefore add the offset to UTC after the date or place a UTC after it (option). In order to output dates as a character string, you can use the functions Format$() and Str$(), which take the current locale into account - in contrast to the function CString(). When using the format function, you should also take a look at the date and time constants at http://gambaswiki.org/wiki/cat/constant, which use predefined format strings.In the `Date` class of the gb.util component, you will find several functions with which you can convert dates from and to UTC, for example.
If you convert a character string or a floating point number into a valid date with the function CDate(Expression AS Variant), it is assumed that no locale is taken into account for the date specification! For the character string, the American format for a date specification must be used: `mM/dD/yyY hh:mm:ss`, with the month before the day. Attention: If you print dates in the console of the IDE, they will always be displayed in the format according to the locale, because the print statement internally uses the function Str$(), which takes the current locale into account!
Print CDate("04/10/2019 11:45:30")
Print CDate(2490688.48993056)
Print Date.ToUTC(CDate("04/10/2019 11:45:30")); " (UTC)"
Print Date.ToUTC(CDate(2490688.48993056)); " (UTC)"
Output: 10.04.2019 13:45:30 Output: 10.04.2019 13:45:30 Output: 10.04.2019 11:45:30 (UTC) Output: 10.04.2019 11:45:30 (UTC)
To convert a local date - given in a string - into a valid date, you should use the function Val() and precede it with a check with IsDate(). Alternatively, you can use the Date() function if the date consists of the different components.
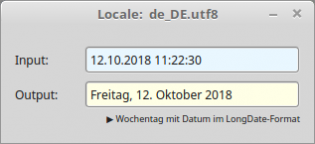
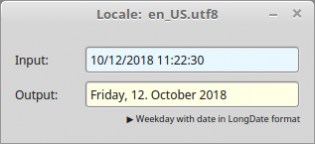
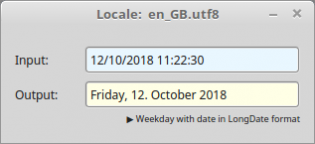
Public Sub TextBox1_Activate() Dim dDate As Date, sMessage As String If Not IsDate(TextBox1.Text) Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= "No date - related to the current locale." Message.Error(sMessage) Else dDate = Val(TextBox1.Text) Print "Locale: " & System.Language ' AUSGABEN Print Format$(dDate, gb.ShortDate) Print Format$(dDate, gb.MediumDate) Print Format$(dDate, gb.LongDate) Print Format$(dDate, "dddd, dd. mmmm yyyy") Print Format$(dDate, "dddd, d. mmmm yyyy") TextBox2.Text = Format$(dDate, "dddd, d. mmmm yyyy") Print Format$(dDate, gb.ShortTime) Print Format$(dDate, gb.MediumTime) Print Format$(dDate, gb.LongTime) Print Subst$(("Today is &1, &2 &3, &4"), Format$(dDate, "dddd"), Format$(dDate, "mmmm"), Format$(dDate, "d"), Format$(dDate, "yyyy")) Endif End
Here you are presented with the results:
Figure 11.5.2.8.4: Output depending on the current locale.
Locale: en_US.utf8 10/12/2018 Oct 12 2018 October Friday 12 2018 Friday, 12. October 2018 Friday, 12. October 2018 11:22 11:22 AM 11:22:30 Today is Friday, October 12, 2018
Figure 11.5.2.8.5: Output depending on the current locale
Locale: en_GB.utf8 12/10/2018 12 Oct 2018 Friday 12 October 2018 Friday, 12. October 2018 Friday, 12. October 2018 11:22 11:22 am 11:22:30 Today is Friday, October 12, 2018
Figure 11.5.2.8.6: Output depending on the current locale
Locale: de_DE.utf8 12.10.2018 12 Okt 2018 Freitag 12 Oktober 2018 Freitag, 12. Oktober 2018 Freitag, 12. Oktober 2018 11:22 11:22 11:22:30 Heute ist Freitag, der 12. Oktober 2018
A special feature is the translation in the last lines, because the function Subst$() allows translations that also take the grammar into account. The following source text excerpt
Print Subst$(("Today is &1, &2 &3, &4"), Format$(dDate, "dddd"), Format$(dDate, "mmmm"), Format$(dDate, "d"), Format$(dDate, "yyyy"))
is shown like this in the translation dialogue:
Standard: Today is &1, &2 &3, &4 German (Germany): Heute ist &1, der &3. &2 &4