Seitenleiste
Inhaltsverzeichnis
25.2.2 Klasse Polygon
Die Klasse Polygon (gb.clipper) repräsentiert ein Polygon. In diesem Kapitel werden Eigenschaften und Methoden der Klasse Polygon vorgestellt.
25.2.2.1 Eigenschaften
Die Klasse Polygon verfügt über diese vier Eigenschaften:
Tabelle 25.2.2.1.1 : Eigenschaften der Klasse Polygon
25.2.2.2 Methoden
Für die Klasse Polygon werden hier alle Methoden beschrieben:
Tabelle 25.2.2.2.1 : Methoden der Klasse Polygon
Hinweise Simplify(..)
- Diese Methode ist wichtig bei sogenannten nicht-einfachen Polygonen. Das sind Polygone, deren Seiten einander schneiden und nicht nur in den Eckpunkten berühren.
- Ein Pentagramm zum Beispiel ist ein klassisches nicht-einfaches Polygon. Die Fill-Regel bestimmt dann, ob das Fünfeck, das innerhalb des Pentagramms entsteht, zum „Inneren“ des Polygons gehört oder zum „Äußeren“. Wenn das Polygon konstruiert wird, gehört das Fünfeck zuerst zum Inneren. Die Simplify()-Methode kann dann, wenn gewünscht, mit einer geeigneten Fill-Regel aufgerufen werden, um das Fünfeck zu entfernen.
Hinweise Clean(..)
- Ecken sind halb-angrenzend, wenn zwischen ihnen genau eine weitere Ecke liegt.
- Der Distance-Parameter ist standardmäßig √2 , so dass eine Ecke entfernt wird, sobald eine angrenzende oder halb-angrenzende Ecke existiert, deren x- und y-Koordinaten nicht mehr als eine Einheit des Koordinatensystems auseinander liegen. Wenn die Ecken halb-angrenzend sind, so wird auch die zwischen ihnen liegende Ecke entfernt.
- Distance ist hier also eine Toleranz-Schranke. Die Clean()-Methode nimmt eventuell Änderungen des Polygons vor, um es danach stärker vereinfachen zu können. Distance gibt auch an, wie weit Punkte verschoben werden dürfen, um stärkere Vereinfachungen des Polygons zu ermöglichen.
25.2.2.3 Beispiele
Diese Klasse ist erstellbar und kann wie ein Array benutzt werden:
Dim PolygonA, PolygonB As Polygon PolygonA = New Polygon ' Polygon mit 0 Ecken PolygonB = New Polygon(7) ' Polygon mit 7 Ecken
So definieren Sie ein Polygon (Pentagramm) mit 5 Eckpunkten (Index 0..4) und lesen aus diesem Polygon die Anzahl der Ecken, die Orientierung und die Koordinaten für alle Eckpunkte aus:
Public Sub ScriptPentagram() Dim iIndex As Integer Dim Point As PointF Dim pPolygon As New Polygon pPolygon.Add(128, 196) pPolygon.Add(412, 196) pPolygon.Add(183, 27) pPolygon.Add(270, 300) pPolygon.Add(357, 27) Print "Anzahl der Eckpunkte = "; pPolygon.Count Print "Orientierung = "; pPolygon.Orientation ' Auslesen aller Eck-Punkte und Anzeige der x,y-Koordinaten der Eck-Punkte des Polygons For iIndex = 0 To pPolygon.Max Point = pPolygon[iIndex] Print "Punkt"; iIndex + 1; "(x) = "; Point.X; " Punkt"; iIndex + 1; "(y) = "; Point.Y Next ' iIndex GenerateNewPicture() SetPictureBorder() Paint.Begin(hPicture) Paint.Translate(xTranslate, yTranslate) Paint.Scale(xScale, yScale) ' +y ▲ Paint.AntiAlias = False DrawCoordinateSystem() ' +y ▲ Paint.Brush = Paint.Color(Color.Red) DrawPolygon(pPolygon, "s") ' Argument 's' → Linien zeichnen, 'f' Fläche füllen Paint.End End ' ScriptPentagram()
Hier sehen Sie die Ausgaben in der Konsole der IDE:
Anzahl der Eckpunkte = 5 Orientierung = False Punkt1(x) = 128 Punkt1(y) = 196 Punkt2(x) = 412 Punkt2(y) = 196 Punkt3(x) = 183 Punkt3(y) = 27 Punkt4(x) = 270 Punkt4(y) = 300 Punkt5(x) = 357 Punkt5(y) = 27
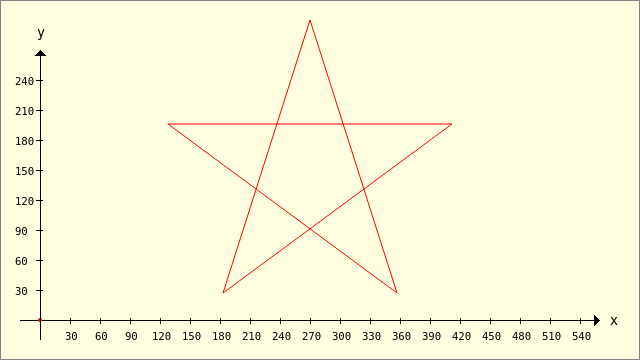
Die Bilder des speziellen Polygons (→ Pentagramm) wurden einerseits mit allen Verbindungslinien gezeichnet und andererseits als Bild mit der Füllfarbe rot:
Abbildung 25.2.2.3.1: Pentagramm (Verbindungslinien)
Abbildung 25.2.2.3.2: Pentagramm-Fläche