GAMBAS-BUCH 3.19.5

Die Klasse Clipper (gb.clipper) implementiert Clipping-Methoden für Polygone.

Die Klasse Clipper verfügt über diese Methoden. Beachten Sie die optionalen Argumente, die mit blauer Farbe markiert sind:

Methode	Beschreibung
Clean( Polygons As Polygon[] [ , Distance As Float ] ) As Polygon[]	Entfernt Ecken, die kollineare Seiten verbinden (an denen die beteiligten Polygone keine echten „visuellen“ Ecken haben) oder fast-kollineare Seiten verbinden (in dem Sinne, dass die Seiten kollinear sind, wenn die Ecke höchstens um Distance verschoben wird) oder die nur höchstens Distance-weit von einer angrenzenden Ecke entfernt sind oder die nur höchstens Distance-weit von einer halb-angrenzenden Ecke entfernt sind – zusammen mit der zwischen ihnen liegenden Ecke.
Difference( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[]	Berechnet mit der Difference-Methode ein Array aus Polygonen und gibt dieses zurück. Argumente der Difference-Funktion sind Polygone in einem Array aus Polygonen und ein Clip vom Datentyp Polygon. Fill ist die zu verwendende Polygon-Füllregel.
ExclusiveOr( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[]	Berechnet mit der ExclusiveOr-Methode ein Array aus Polygonen und gibt dieses zurück. Argumente der ExclusiveOr-Funktion sind Polygone in einem Array aus Polygonen und ein Clip vom Datentyp Polygon. Fill ist die zu verwendende Polygon-Füllregel.
Intersection ( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[]	Berechnet mit der Intersection-Methode ein Array aus Polygonen und gibt dieses zurück. Argumente der Intersection-Funktion sind Polygone in einem Array aus Polygonen und ein Clip vom Datentyp Polygon. Fill ist die zu verwendende Polygon-Füllregel.
Union ( Polygons As Polygon[] [ , Clip As Polygon[], Fill As Integer ] ) As Polygon[]	Berechnet mit der Union-Methode ein Array aus Polygonen und gibt dieses zurück. Argumente der Union-Funktion sind Polygone in einem Array aus Polygonen und ein Clip vom Datentyp Polygon. Fill ist die zu verwendende Polygon-Füllregel.
Simplify ( Polygons As Polygon[] [ , Fill As Integer ] ) As Polygon[]	Entfernt alle Selbst-Überschneidungen der Polygone unter Verwendung der Operation 'Union' anhand des angegebenen Fill-Typs. Wenn sich innerhalb eines Polygons zwei Ecken berühren, dann wird das Polygon in zwei Polygone geteilt. Beachten Sie den Datentyp: Array aus Polygonen

Tabelle 25.2.1.1.1 : Methoden der Klasse Clipper

Jedes Polygon oder eine Anordnung von Polygonen muss einen Fülltyp beim Aufruf einer der folgenden Clipping-Methoden besitzen: Difference, Union, Intersection oder ExclusiveOr.

Für die Klasse Clipper werden hier die Konstanten für die Polygon-Füllregeln und die Verbindungs-Typen beschrieben.

Tabellen 25.2.1.2.1 : Konstanten der Klasse Clipper

Um alle Beispiele nachvollziehen zu können, finden Sie im Download-Bereich ein Projekt-Archiv. Auch für die speziellen Polygone 'Rechteck' → Kapitel 25.2.4 Klassen Rect und RectF finden Sie die im genannten Kapitel genutzten Quelltexte. Aus diesem Grund wird weitgehend auf die kompletten Beispiel-Quelltexte verzichtet. Es werden nur Quelltext-Ausschnitte vorgestellt und die erzielten Ergebnisse angezeigt. Es wird dabei grundsätzlich auf ein Picture gezeichnet, das dann in einer DrawArea angezeigt wird. Nur so ist es möglich, sich auch die Ergebnisse beim Einsatz der Methoden Clipper.Intersection, Clipper.Union, Clipper.ExclusiveOr oder Clipper.Difference anzusehen.

Beispiel 1

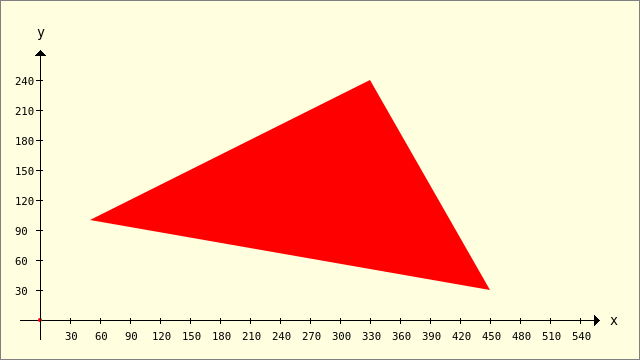
Im ersten Beispiel wird ein Dreieck als konkaves Polygon vorgestellt. Ein Polygon ist konkav, wenn alle Verbindungslinien im Polygon stets im Inneren des Polygons liegen.

• Zuerst wird ein Polygon mit vier Ecken erzeugt und die Koordinaten eines ausgewählten Punktes auf unterschiedliche Art ausgelesen und angezeigt.
• Anschließend wird ein Punkt mit der Methode Clipper.Remove(point_index) entfernt und das reduzierte Polygon einem anderen Polygon pTriangel zugewiesen. Dessen Punkte werden ausgelesen und angezeigt; ebenso die Fläche des Polygons.
• Abschließend wird das Polygon angezeigt.

Public Sub ScriptPolygon1()
  Dim iIndex As Integer  
  Dim pPolygon, pTriangle As New Polygon
  Dim Point As New PointF 
 
  pPolygon.Add(50, 100)      ' A
  pPolygon.Add(450, 30)      ' B
  pPolygon.Add(330, 240)     ' C
  pPolygon.Add(70, 123.4)    ' D
 
' Auslesen des 4. Eck-Punktes (Index=3) und Anzeige der Koordinaten Dx und Dy
  Point = pPolygon[3]
  Print "Dx = "; Point.X
  Print "Dy = "; Point.Y
  Print "Dx = "; pPolygon[3].X ' Alternative
  Print "Dy = "; pPolygon[3].Y
 
' Der Punkt D(Index=3) wird aus dem Polygon entfernt
  pPolygon.Remove(3, 1)
  pTriangle = pPolygon
 
' Auslesen aller Eck-Punkte und Anzeige der Koordinaten des Dreiecks
  For iIndex = 0 To pTriangle.Max
    Point = pTriangle[iIndex]
    Print "Punkt"; iIndex + 1; ".x = "; Point.X; " Punkt"; iIndex + 1; ".y = "; Point.Y
  Next ' iIndex
' Berechnung und Anzeige der Fläche des Polygons
  Print "Das Dreieck ABC hat eine Fläche von "; Round(pTriangle.Area, 2); " Flächen-Einheiten!"
 
  GenerateNewPicture()
  SetPictureBorder()  
  Paint.Begin(hPicture)   
    Paint.Translate(xTranslate, yTranslate)
    Paint.Scale(xScale, yScale) ' +y ▲
    Paint.AntiAlias = False
    DrawCoordinateSystem() ' +y ▲
    Paint.Brush = Paint.Color(Color.Red)
      DrawPolygon(pTriangle, "f")
    Paint.AntiAlias = True
  Paint.End
End ' ScriptPolygon1

Das sind die Ausgaben in der Konsole der IDE:

Dx = 70
Dy = 123,4
Dx = 70
Dy = 123,4
Punkt1.x = 50  Punkt1.y = 100
Punkt2.x = 450 Punkt2.y = 30
Punkt3.x = 330 Punkt3.y = 240
Das Dreieck ABC hat eine Fläche von 37800 Flächen-Einheiten!

Abbildung 25.2.1.3.1: Polygon 'Dreieck'

Beispiel 2

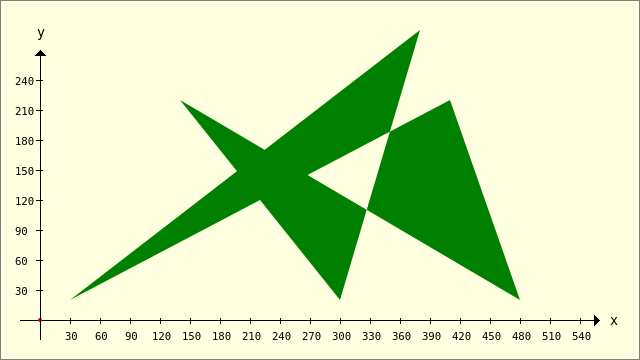
Hier wird nur ein konvexes Polygon vorgestellt:

Abbildung 25.2.1.3.2: Konvexes Polygon

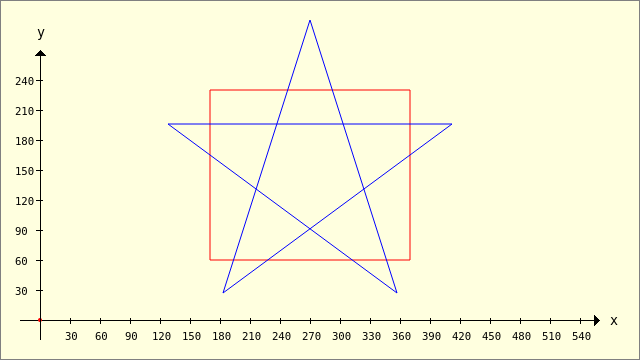
Für die nächsten vier Beispiele werden stets die gleichen Polygone verwendet – ein Pentagramm und ein Rechteck. Dann werden nacheinander die 4 Methoden

• Clipper.Intersection,
• Clipper.Union,
• Clipper.ExclusiveOr und
• Clipper.Difference

eingesetzt für vier jeweils unterschiedliche Füll-Regeln, die wesentlich das Ergebnis bestimmen.

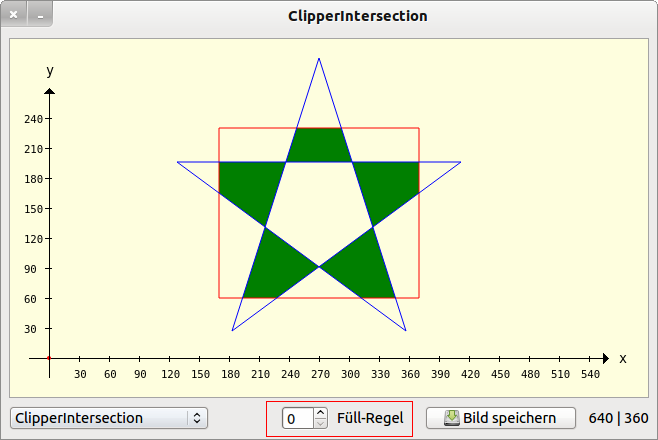
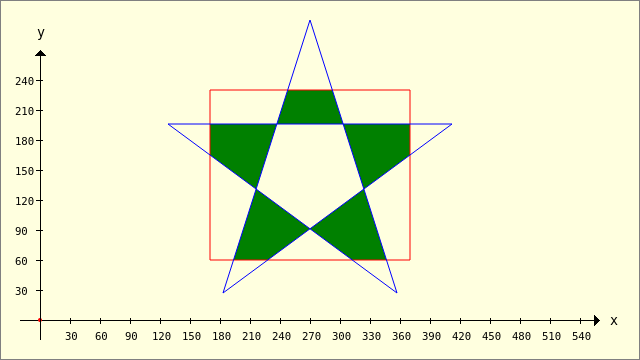
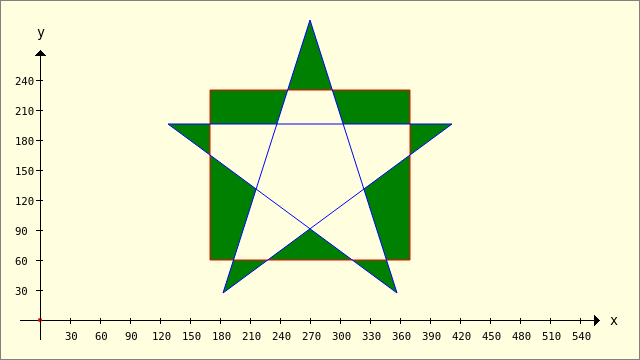
Beispiel 3 – Clipper.Intersection(..)

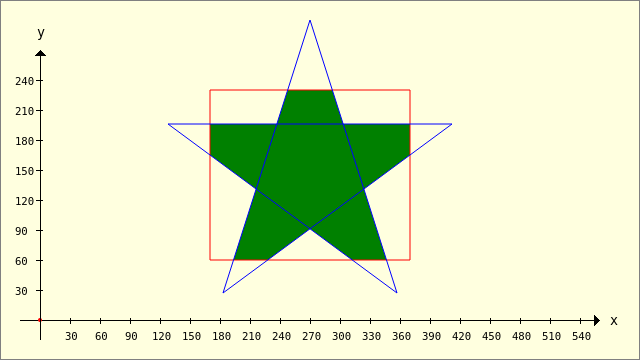
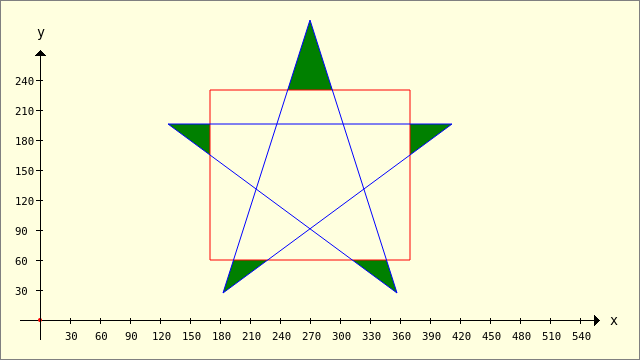
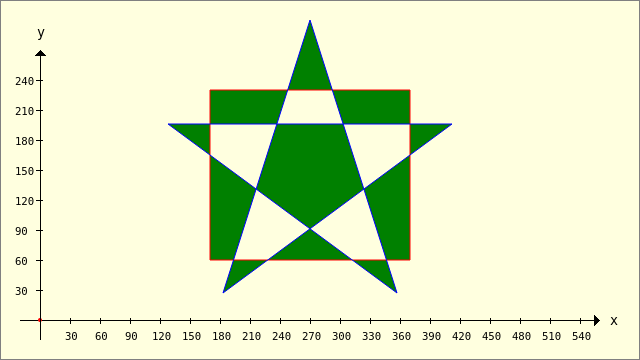
Public Sub ScriptCIntersection()
  Dim pPentagramm, pRectangle, hP As New Polygon
 
  pPentagramm.Add(128, 196)
  pPentagramm.Add(412, 196) 
  pPentagramm.Add(183, 27) 
  pPentagramm.Add(270, 300) 
  pPentagramm.Add(357, 27) 
 
  pRectangle.Add(170, 230)
  pRectangle.Add(370, 230)
  pRectangle.Add(370, 60)
  pRectangle.Add(170, 60)
 
  GenerateNewPicture()
  SetPictureBorder()  
  Paint.Begin(hPicture)   
    Paint.Translate(xTranslate, yTranslate)
    Paint.Scale(xScale, yScale) ' +y ▲
    Paint.AntiAlias = False
    DrawCoordinateSystem() ' +y ▲       
 
    Paint.Background = Color.DarkGreen
    For Each hP In Clipper.Intersection([pPentagramm], [pRectangle], sbFillRule.Value) ' 0..3
      DrawPolygon(hP)
    Next ' hP
 
    Paint.Brush = Paint.Color(Color.Red)
    DrawPolygon(pRectangle, "s")
    Paint.Brush = Paint.Color(Color.Blue)
    DrawPolygon(pPentagramm, "s")    
  Paint.End 
 
End ' ScriptCIntersection()

Abbildung 25.2.1.3.3: Intersektion – Auswahl Füll-Regel (0..3)

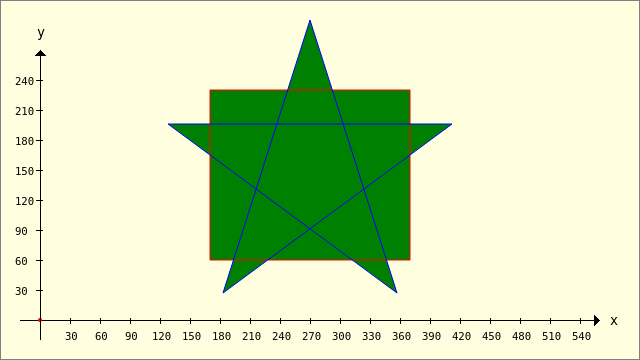
Abbildung 25.2.1.3.4: Intersektion – Füll-Regel 0 (FillEvenOdd)

Abbildung 25.2.1.3.5: Intersektion – Füll-Regel 1 (FillNonZero)

Beispiel 4 – Clipper.Difference(..)

Abbildung 25.2.1.3.6: Differenz – Füll-Regel 0 (FillEvenOdd)

Abbildung 25.2.1.3.7: Differenz – Füll-Regel 2 (FillPositive)

Beispiel 5 – Clipper.ExclusiveOr(..)

Abbildung 25.2.1.3.8: ExklusivOder – Füll-Regel 0 (FillEvenOdd)

Abbildung 25.2.1.3.9: ExklusivOder – Füll-Regeln 1 und 3

Beispiel 6.1 – Clipper.Union(..)

Für die Illustration des Einsatzes der Methode Clipper.Union(..) wird nur eine Abbildung gezeigt, weil die Bilder für die Füll-Regel 0, 1 und 3 gleich sind:

Abbildung 25.2.1.3.10: Union – Füll-Regel 0 (FillEvenOdd)

Beispiel 6.2 – Clipper.Union(..)

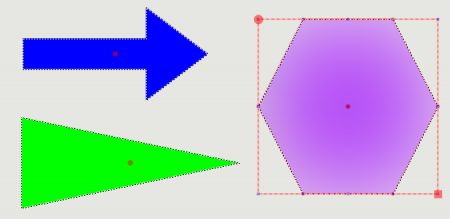
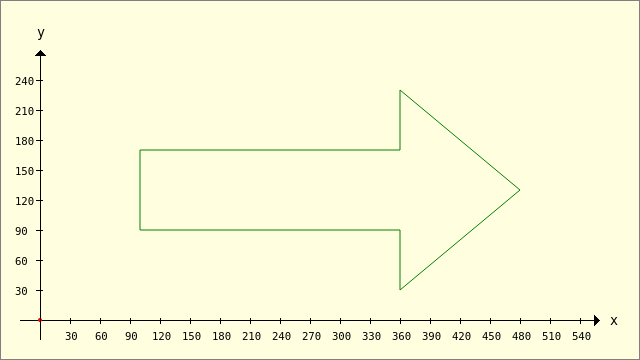
Mit Hilfe der Methode Clipper.Union(..) können Sie beispielsweise Formen wie ein Rechteck und ein Dreieck zu einem Pfeil zusammenzusetzen (Vereinigung von Polygonen) und als Einheit – als ein geometrisches Objekt – zu betrachten.

Abbildung 25.2.1.3.11: Verwendung: Formen aus dem Bild-Editor der Gambas-IDE

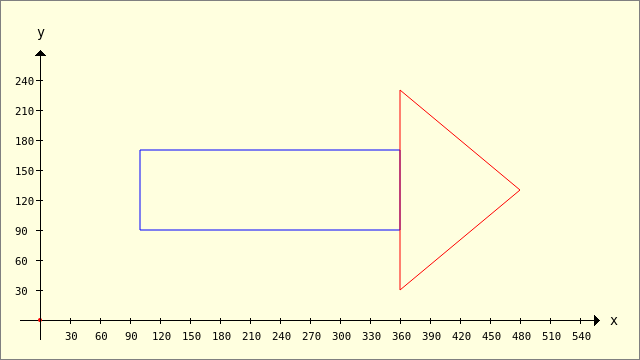
Abbildung 25.2.1.3.12: Ein Dreieck und ein Rechteck

Abbildung 25.2.1.3.13: Ein Pfeil (Hüll-Kurve)

Mit diesem Quelltext erzeugen Sie die Abbildung → 25.2.1.3.12, der auch die (auskommentierte) Alternative zeichnen lässt:

Public Sub ScriptPolygon2()
  Dim iIndex As Integer
  Dim Point As New PointF
  Dim pPolygon, pTriangle, hP As New Polygon
  Dim aPolygon As Polygon[]
 
  pPolygon.Add(100, 170)  ' A
  pPolygon.Add(360, 170)  ' B
  pPolygon.Add(360, 90)   ' C
  pPolygon.Add(100, 90)   ' D
 
  pTriangle.Add(360, 230) ' P 
  pTriangle.Add(480, 130) ' Q
  pTriangle.Add(360, 30)  ' R
 
  aPolygon = Clipper.Union([pPolygon], [pTriangle], 0)
 
  GenerateNewPicture()
  SetPictureBorder()  
  Paint.Begin(hPicture)   
    Paint.Translate(xTranslate, yTranslate)
    Paint.Scale(xScale, yScale) ' +y ▲
    Paint.AntiAlias = False
    DrawCoordinateSystem() ' +y ▲      
    Paint.Brush = Paint.Color(Color.DarkGreen)
 
  ' Rechteck und Dreieck 
    Paint.Brush = Paint.Color(Color.Blue)
    DrawPolygon(pPolygon, "s")
    Paint.Brush = Paint.Color(Color.Red)
    DrawPolygon(pTriangle, "s")
 
  ' Pfeil als Einheit 
  ' For Each hP In aPolygon
  '   DrawPolygon(hP, "s")
  ' Next    
  Paint.End
 
End ' ScriptPolygon2()