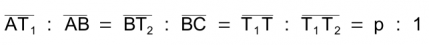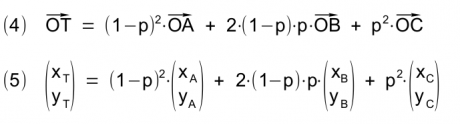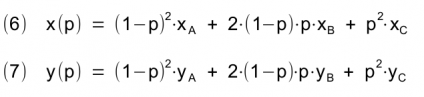GAMBAS-BUCH 3.19.1

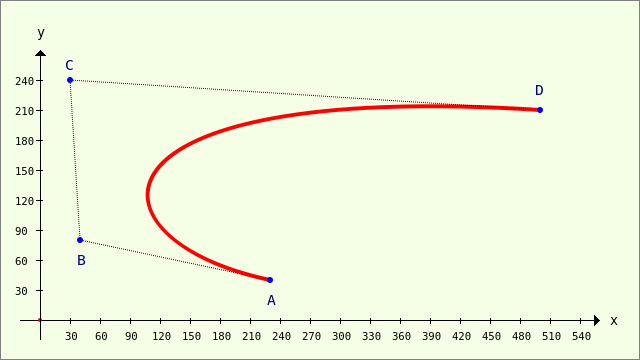
Die CurveTo-Methode der Klasse Paint verwendet zum Zeichnen → Kapitel 23.3.5.3 'Bézier-Kurven' Bézier-Kurven dritten Grades, die durch 4 Punkte bestimmt werden. Zwei Punkte (A und D) bestimmen den Anfangs- und Endpunkt der Kurve, deren Krümmungsverhalten Sie über die Lage aller 4 Punkte A, B, C und D → Abbildung 23.3.8.1 festlegen. Die Punkte B und C werden Stützpunkte genannt.

Abbildung 23.3.9.1: Bézier-Kurve 3. Grades (4 Punkte)

In diesem Kapitel wird der Versuch unternommen, aus der geometrischen Definition einer Bézier-Kurve 2. Grades – für die es ja in der Klasse Paint keine Methode gibt – eine analytische Beschreibung einer Bézier-Kurve 2. Ordnung zu entwickeln. Damit wird die Erwartung verknüpft, dass Sie die Arbeit mit Bézier-Kurven 3. Grades besser verstehen, weil die Theorie von ähnlichen Ansätzen ausgeht.

Mit den gewonnenen expliziten Parameter-Gleichungen sowie den Methoden der Klasse Paint werden einige Bézier-Kurven 2. Grades gezeichnet.

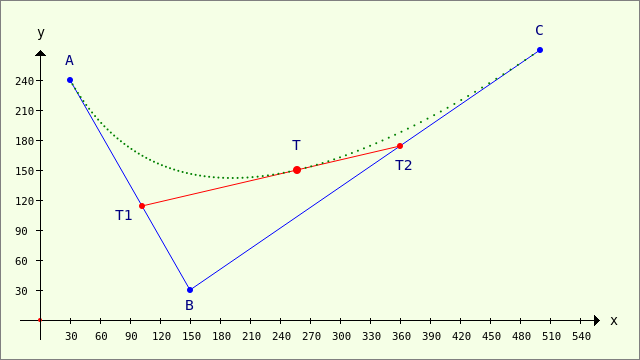
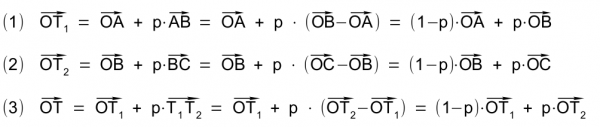
Gegeben sind drei (verschiedene) Punkte A, B und C in einer (Koordinaten-)Ebene mit einer (normierten) Vektorbasis. Die Punkte A, B und C werden in der gezeigten Art verbunden. Auf den Verbindungslinien AB und BC existieren die beiden Teilungspunkte T1 und T2, auf deren Verbindungslinie T1T2 der Punkt T liegt:

Abbildung 23.3.9.1.1: Bézier-Kurve – Definition 2. Grades (3 Punkte)

Für die drei Teilungspunkte T1, T2 und T gilt folgende Festlegung, die jeweils ihre Lage auf den Verbindungslinien bestimmt:

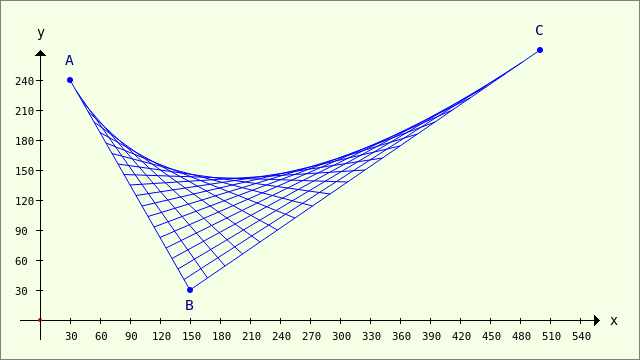
Für jeden reellen Parameterwert p aus dem Intervall [0|1] ist T ein so genannter Bézier-Punkt. Die Menge aller Punkte T=T(p) ergibt die Bézier-Kurve AC von A nach C mit T(0) = A und T(1) = C. Die punktierte grüne Linie besteht aus ausgewählten Punkten der Bézier-Kurve AC. Zeichnet man für ausgewählte Parameter p die Verbindungslinien der Punkte TiTj , dann entsteht dieses Bild:

Abbildung 23.3.9.1.2: Darstellung von Verbindungslinien TiTj

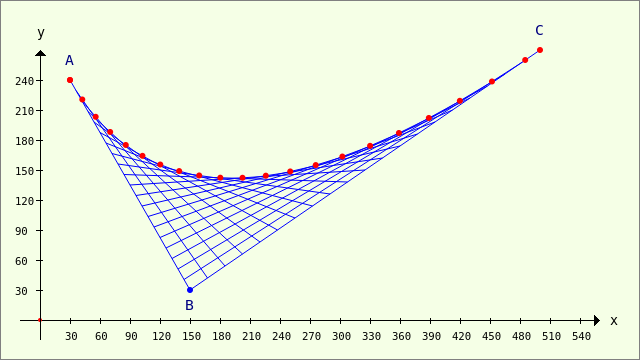
Sie können schon sehr deutlich die Hüllkurve aller Verbindungslinien der Punkte TiTj 'sehen'. Der Eindruck wird noch verstärkt, wenn die definierten Bézier-Punkte T auf den Verbindungslinien zusätzlich in rot eingezeichnet werden:

Abbildung 23.3.9.1.3: Bézier-Punkte

Gesucht ist eine analytische Beschreibung für die Koordinaten der Bézier-Punkte T = T(p) für jeden Parameterwert p aus dem Intervall 0 ≤ p ≤ 1 auf der Bézier-Kurve von A nach C:

Aus den beiden Vektor-Gleichungen 1 und 2 gewinnt man die Gleichung 4 beziehungsweise 5, wenn man die Gleichungen 1 und 2 in 3 einsetzt:

Aus der Gleichung 5 entstehen die beiden (expliziten) Parameter-Gleichungen 6 und 7 für die Berechnung der x- und y-Koordinate eines Bézier-Punktes der quadratischen Bézier-Kurve (2. Grades) zwischen den Punkten A und C, deren Krümmungsverhalten durch die Lage des Punktes B definiert wird:

Beispiel 1

Die Bézier-Kurve AB mit dem Stützpunkt B wird unter Verwendung der Gleichungen 6 und 7 und Methoden der Klasse Paint gezeichnet:

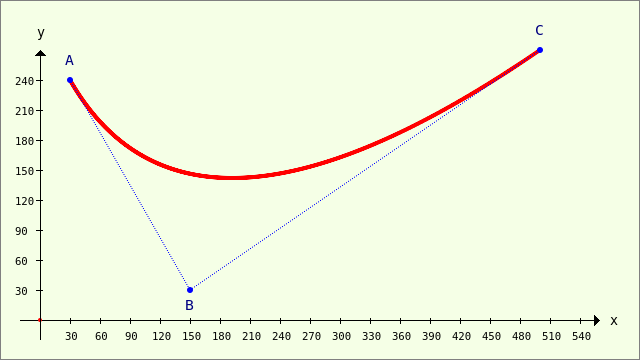
Abbildung 23.3.9.3.1: Bézier-Kurve AC – B(150|30)

Im folgenden Quelltext werden die Punkte A, B und C über globale Variablen vom Daten-Typ PointF deklariert und die beiden Gleichungen 6 und 7 als Funktionen implementiert:

[1] Public A As PointF 
[2] Public B As PointF
[3] Public C As PointF
[4] 
[5] Public Sub Form_Open()
[6]   …  
[7]   A = New PointF
[8]   A.x = 30
[9]   A.y = 240
[10]   B = New PointF(150, 30) ' Alternative Angabe der Koordinaten eines Punktes
[11]   C = New PointF(500, 270)
[12]   …
[13] End ' Form_Open()
[14] 
[15] Public Function BézierX(p As Float, AX As Float, BX As Float, CX As Float) As Float  
[16] ' Analytische Beschreibung x(p) einer Bézier-Kurve 2. Grades (3 Punkte)  
[17]   Return (1 - p) * (1 - p) * AX + 2 * (1 - p) * p * BX + p * p * CX  
[18] End ' BézierX(..)
[19] 
[20] Public Function BézierY(p As Float, AY As Float, BY As Float, CY As Float) As Float  
[21] ' Analytische Beschreibung y(p) einer Bézier-Kurve 2. Grades (3 Punkte)  
[22]   Return (1 - p) * (1 - p) * AY + 2 * (1 - p) * p * BY + p * p * CY
[23] End ' BézierY(..)

Die Prozedur PaintScriptBézier3Points() zum Zeichnen einer Bézier-Kurve 2. Grades nutzt die Prozeduren, die schon in den Projekt-Beispielen im → Kapitel 23.3.3 verwendet wurden:

[1] Public Sub PaintScriptBezier3Points()
[2]   Dim k As Integer
[3]   Dim p As Float
[4]   Dim vP As Vector
[5]   
[6]   GenerateNewPicture()
[7]   SetPictureBorder()  
[8]   Paint.Begin(hPicture) 
[9]     Paint.Translate(xTranslate, yTranslate)
[10]     Paint.Scale(xScale, yScale) ' +y ▲  
[11]     DrawCoordinateSystem()
[12]      
[13]   ' PARABEL-STÜCK
[14]     Paint.Brush = Paint.Color(Color.Red)
[15]     Paint.Brush = Paint.Color(Color.Red)
[16]     For k = 0 To (C.x - A.x)
[17]         p = k / 470
[18]         Paint.Arc(BézierX(p, A.x, B.x, C.x), BézierY(p, A.y, B.y, C.y), 2)
[19]     Next
[20]     Paint.Fill()
[21] 
[22]   ' Verbindungslinien A-B-C
[23]     Paint.Brush = Paint.Color(Color.Blue)
[24]     Paint.LineWidth = 1
[25]     Paint.Dash = [1, 1]
[26]     Paint.MoveTo(A.x, A.y)
[27]     Paint.LineTo(B.x, B.y)
[28]     Paint.LineTo(C.x, C.y)
[29]     Paint.Stroke
[30]     Paint.Dash = Null
[31] 
[32]   ' Punkte A, B und C
[33]     Paint.Arc(A.x, A.y, 3)
[34]     Paint.Arc(B.x, B.y, 3)
[35]     Paint.Arc(C.x, C.y, 3)
[36]     Paint.Fill
[37] 
[38]   ' TEXT
[39]     Paint.NewPath
[40]     Paint.Scale(1, -1) ' +y ▼
[41]       Paint.Font = Font["Monospace, 11"]
[42]       Paint.Brush = Paint.Color(Color.DarkBlue)
[43]       Paint.DrawText("A", 25, -255)
[44]       Paint.DrawText("B", 145, -10)     
[45]       Paint.DrawText("C", 495, -285)
[46]     Paint.Scale(1, -1) ' +y ▲  
[47]   Paint.End
[48]   
[49] End ' PaintScriptBezier3Points()

Kommentar:

• Die Bézier-Kurve wird in den Zeilen 15 bis 20 als Punktfolge gezeichnet.
• Mit den beiden Funktionen BézierX(..) und BézierY(..) werden die Koordinaten Tx und Ty jedes Bézier-Punktes T = T(p) im Intervall 0 ≤ p ≤ 1 berechnet (T(0) = A und T(1) = C).
• Das Parameter-Intervall von 0 ≤ p ≤ 1 wird in den Zeilen 16 und 17 für das Zeichnen der Bézier-Punkte auf das Intervall 0 ≤ x ≤ (C.x-A.x) abgebildet.
• In der Zeile 18 wird ein Bézier-Punkt T(p) mit den Koordinaten Tx und Ty als Kreis mit sehr kleinem Radius gezeichnet.
• In den weiteren Anweisungen ab Zeile 22 werden die Verbindungslinien AB und BC sowie die Punkte A, B und C gezeichnet. Abschließend werden die drei Punkte noch bezeichnet – jedoch ohne die Angabe von Koordinaten.

Beispiel 2

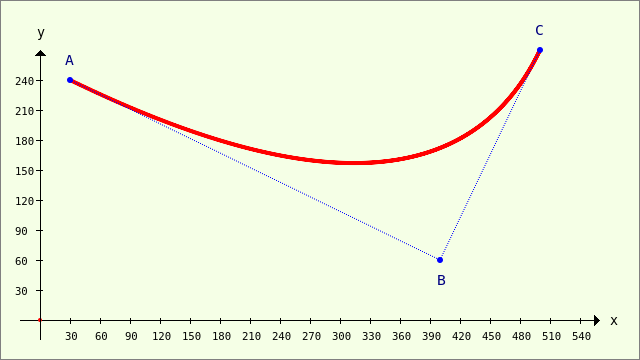
Abbildung 23.3.9.3.2: Bézier-Kurve – B(400|60)

Im zweiten Beispiel werden die Koordinaten des Stützpunktes B geändert. Die Koordinaten des Anfangspunktes A und des Endpunktes C bleiben gegenüber dem Beispiel 1 unverändert. Sehr deutlich ist der Einfluss des Punktes B auf den Kurvenverlauf der Bézier-Kurve zu sehen. Im Projekt 'BézierExkurs' können Sie die Koordinaten von B in weiten Grenzen ändern, um die Wirkung der Veränderung sofort zu sehen.