GAMBAS-BUCH 3.19.5

Dieses Kapitel basiert auf Vorschlägen und Projekten von Tobias Boege und Ingo Beckert zur perspektivischen Anzeige von Bildern mit Tiefenwirkung. In beiden Projekten werden die Image-Matrizen in Abhängigkeit von einem Drehwinkel φ so geändert, das eine perspektivische Anzeige gelingt.

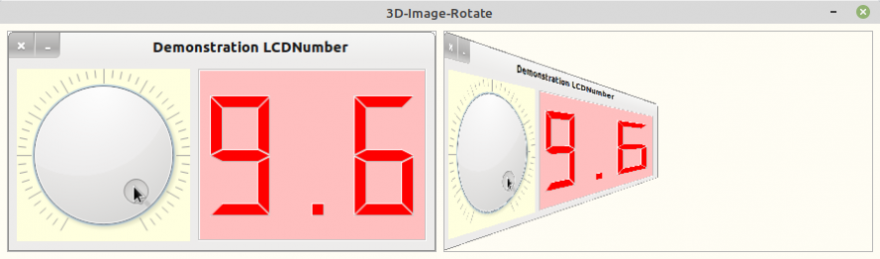
Abbildung 23.2.4.10.1.1: Horizontale Stauchung (φ=60°)

Wenn Sie ein Bild verzerren, respektive stauchen oder strecken möchten und zwar Teile des Bildes unterschiedlich stark – je nachdem, ob sie weiter links oder rechts beziehungsweise oben oder unten im Bild liegen – so ist das kein leichtes Unterfangen. Einfacher wird es, wenn angenommen wird, dass eine Ebene E im Raum R3 existiert und E auf eine andere Ebene E' abgebildet werden soll. Der Raum R3 ist das kartesische Koordinatensystem und die Ebene E, in der das Bild liegt, sei die Ebene, die von der y- und der z-Achse aufgespannt wird. Die Ebene E soll an einer Geraden kreisförmig gedreht werden, ähnlich wie eine Tür um ein Scharnier. Es wird ferner angenommen, dass die untere linke Ecke des Bildes im Koordinatenursprung O(0,0,0) liegt und sich das Bild in die positive z- und y-Richtung ausdehnt.

Dafür gilt die folgende Abbildungsgleichung E': [ x → x + cos(φ), y → y·sin(φ), z → z ]. Die Ebene E ist die y,z-Ebene und damit ist x = 0. Man erhält eine um den Winkel φ gedrehte Ebene mit arc(φ)∈R sowie 0⇐arc(φ)⇐ Pi/2. Die Einschränkung für φ ist verständlich, weil das Bild ja keine Rückseite hat, die betrachtet werden könnte. Jetzt liegt das Bild also quer im Raum und Sie müssen die Koordinaten der neuen Ebene E' so in ein Image-Objekt übersetzen, als ob aus der Sicht der originalen Ebene E geschaut wird.

Dafür wird der Raum R3 verlassen, der am Anfang nur der Anschaulichkeit wegen betrachtet wurde. Sie sehen sofort: Die z-Koordinate kann vernachlässigt werden und es geht zurück in den R2. Das Image liegt somit in x,y-Koordinaten vor.

Für die Abbildungsgleichung einer Stauchung nur in x-Richtung (horizontal) gilt nun E': [ x → x·cos(φ), y → y ].

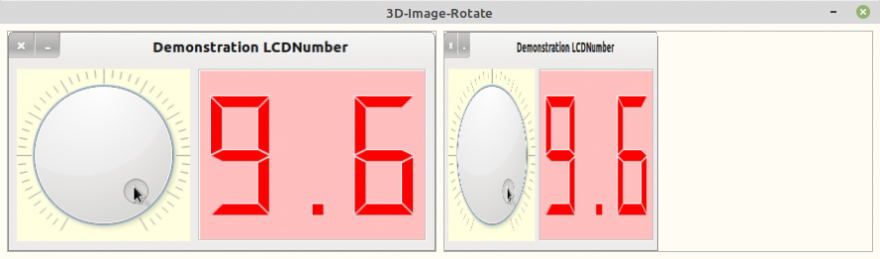
Abbildung 23.2.4.10.1.2: Horizontale Stauchung (φ=60°)

Bisher wurde das Bild mit dem Winkel φ nur in der Horizontalen gestaucht. Es fehlt noch die vertikale Stauchung, die maßgeblich zur Illusion von Perspektive beiträgt. Durch die Perspektive werden ja die rechten Teile des Bildes weiter 'raumwärts' geschickt und müssen kleiner erscheinen, um Tiefenwirkung zu erreichen.

Jetzt ist noch festzulegen, von wo der Betrachter das Bild anschaut, d.h. wie stark das Bild von oben und unten nur vertikal gestaucht werden soll. Es wird die Bildmitte gewählt und das Bild für eine „perspektivische Stauchung“ von oben und unten in gleichem Maße gestaucht.

Für die vertikale Stauchung kann man einen Faktor ψ definieren, der angibt, wie stark auf der gesamten Bild-Breite das Bild in y-Richtung gestaucht werden soll. Mit dem Faktor ψ = 2·arc(φ)/Pi und ψ in [0,1] bleibt nach der Drehung um φ noch eine Bildhöhe H' = (1-ψ)·H erhalten.

Abbildung 23.2.4.10.1.3: Horizontale und vertikale Stauchung mit ψ=1 und φ=60°

Abbildung 23.2.4.10.1.4: Horizontale und vertikale Stauchung mit ψ=0,666 und φ=60°

Projekte

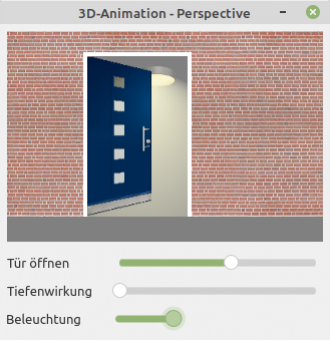
Die Gambas-Buch-Autoren Tobias Boege und Ingo Beckert haben ihre theoretischen Ansätze in zwei Projekten umgesetzt, deren Quelltext-Archive Sie für eigene Erkundungen im Download-Bereich finden.

Das erste Projekt von Tobias Boege folgt direkt den Ausführungen im oberen Absatz, während das zweite Projekt von Ingo Beckert mit einstellbarer Tiefenwirkung arbeitet:

Abbildung 23.2.4.10.1.5: Perspektivische Animation (Ingo Beckert)