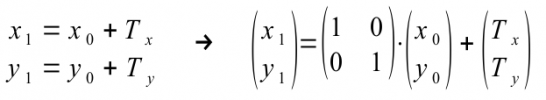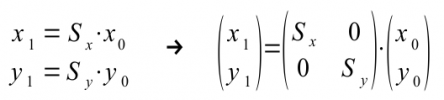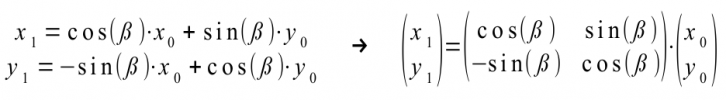Seitenleiste
k23:k23.3:k23.3.8:start
Inhaltsverzeichnis
23.3.8 PaintMatrix
Die Klasse PaintMatrix (gb.qt4) repräsentiert eine Transformationsmatrix die u.a. für die Ausführung affiner Abbildungen (Translation, Skalierung, Rotation) genutzt wird.
Beachten Sie, dass alle Methoden die Ergebnismatrix zurückgeben, so dass Sie in einer Code-Zeile durch Verketten von Methodenaufrufen mehrere Transformationen durchführen können.
23.3.8.1 Erzeugen einer PaintMatrix
Eine neue PaintMatrix kann mit New PaintMatrix ([…]) generiert werden:
Dim hPaintMatrix As PaintMatrix hPaintMatrix = New PaintMatrix ([XX As Float,XY As Float,YX As Float,YY As Float,X0 As Float,Y0 As Float])
Wenn die Matrix-Elemente nicht angegeben werden, so wird eine Einheitsmatrix (Identität) angelegt. Sie können die Klasse auch wie eine statische Funktion einsetzen, die einen Funktionswert vom Typ PaintMatrix besitzt:
Function PaintMatrix ([XX As Float,XY As Float,YX As Float,YY As Float,X0 As Float,Y0 As Float])
23.3.8.2 Methoden
Die Klasse PaintMatrix besitzt nur Methoden.
| Methode | Beschreibung |
|---|---|
| Function Translate ( TX As Float, TY As Float ) As PaintMatrix | Ändert die PaintMatrix um die Verschiebungen TX und TY und gibt die geänderte Matrix zurück. |
| Function Scale ( SX As Float, SY As Float ) As PaintMatrix | Ändert die PaintMatrix mit den Skalierungsfaktoren SX und SY und gibt die geänderte Matrix zurück. |
| Function Rotate ( Angle As Float ) As PaintMatrix | Ändert die PaintMatrix mit dem Drehwinkel (Bogenmaß) und gibt die geänderte Matrix zurück. |
| Function Reset ( ) As PaintMatrix | Setzt die PaintMatrix auf die Identitätsmatrix (Einheitsmatrix) zurück und gibt die geänderte Matrix zurück. |
| Function Multiply ( Matrix2 As PaintMatrix ) As PaintMatrix | Ändert die PaintMatrix durch Multiplikation mit der angegebenen Matrix2 und gibt die geänderte Matrix zurück. |
| Function Invert ( ) As PaintMatrix | Invertiert die Matrix und gibt die geänderte Matrix zurück. Lässt sich die Matrix nicht invertieren, so wird NULL zurückgegeben - was zu prüfen ist. |
| Function Copy ( ) As PaintMatrix | Es wird eine Kopie der aktuellen PaintMatrix als eigenständiges Objekt zurückgegeben. |
| Function Map ( Point As PointF ) As PointF | Wendet die Transformation auf den gegebenen Punkt an (Matrix-Vektor-Produkt) und gibt den Bild-Vektor zurück. |
Tabelle 23.3.8.2.1 : Methoden der Klasse PaintMatrix
23.3.8.3 Hinweise
Für eine Translation eines Punktes P(x0|y0) → P'(x1|y1) in einem kartesischen Koordinatensystem (xy-Ebene E) ergeben sich diese Tranformationsgleichungen für P(x0|y0) als Original-Punkt und mit P'(x1|y1) als Bild-Punkt. Die rechte Gleichung ist die äquivalente Matrix-Schreibweise für die Beschreibung einer Translation oder Verschiebung:
Für alle anderen Punkte der Koordinatenebene E gilt diese Gleichung bei einer Verschiebung um die Verschiebungsweite von Tx in x-Richtung und Ty in y-Richtung ebenso.
Eine Skalierung der Koordinatenachsen kann mit diesen beiden Transformationsgleichungen beschrieben werden, wobei die Faktoren Sx und Sy die Skalierungsfaktoren in beiden Koordinatenrichtungen sind:
Für die Rotation eines Punktes P(x0|y0) um den Koordinaten-Ursprung O(0|0) mit einem Drehwinkel ß verwenden Sie die folgenden Transformationsgleichungen für Original- und Bild-Punkt:
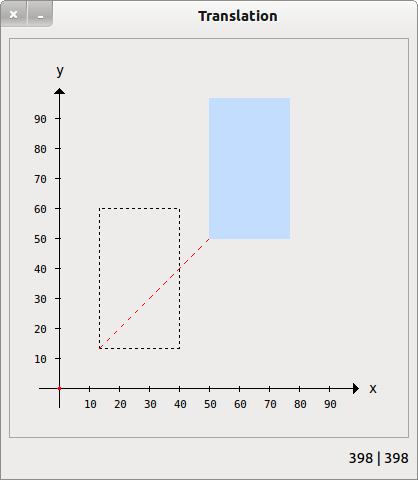
Das folgende Bild zeigt die erzielbare Wirkungen bei einer Translation einer einfachen Grafik:
Abbildung 23.3.8.3.1: Verschiebung eines Rechtecks
Download
k23/k23.3/k23.3.8/start.txt · Zuletzt geändert: 20.06.2016 (Externe Bearbeitung)
Seiten-Werkzeuge
Falls nicht anders bezeichnet, ist der Inhalt dieses Wikis unter der folgenden Lizenz veröffentlicht: CC Attribution-Noncommercial 3.0 Unported
