GAMBAS-BUCH 3.19.5

Mit der CurveTo-Methode der Klasse Paint haben Sie die Möglichkeit, auch gekrümmte Linien zu zeichnen, deren Krümmungsverhalten Sie vorgeben. Die CurveTo-Methode verwendet zum Zeichnen eine Bézier-Kurve dritten Grades, die durch 4 Punkte bestimmt wird. Bézier-Kurven mit einem höheren Grad als 3 sind entbehrlich, weil komplexe Kurven-Bögen aus Teilbögen von Bézier-Kurven 1.-3. Grades zusammengesetzt werden können. Interessante, gut strukturierte Informationen zur Definition und Beschreibung von Bézier-Kurven bieten zum Beispiel diese Webseite http://www.mathepedia.de/Bezierkurven.aspx und www.de.wikipedia.org/wiki/Bezierkurve.

Im → Kapitel 23.3.9 wird der Versuch unternommen, aus der geometrischen Definition einer Bézier-Kurve 2. Grades – für die es ja in der Klasse Paint keine Methode gibt – eine analytische Beschreibung einer Bézier-Kurve 2. Ordnung zu entwickeln. Diese Herleitung bildet die theoretische Grundlage für einen Teil des vorliegenden Projektes, denn es werden u.a. mit den gewonnenen expliziten Parameter-Gleichungen sowie den Methoden der Klasse Paint einige Bézier-Kurven 2. Grades gezeichnet.

Beispiel 1

Im ersten Beispiel wird eine Bézier-Kurve dritten Grades gezeichnet:

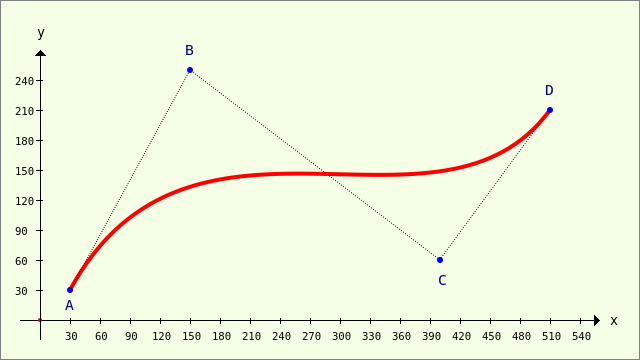
Abbildung 23.3.5.3.1: Modellierte Bézier-Kurve 3. Grades (4 Punkte)

Die Punkte A und D bestimmen den Anfangs- und Endpunkt der Kurve. Das Krümmungsverhalten legen Sie dann über die Lage der Punkte B und D fest → Abbildung 23.3.5.3.1. Es mag Sie verwundern, dass in der Dokumentation für die CurveTo-Methode nur drei Punkte angegeben werden:

CurveTo ( X1 As Float, Y1 As Float, X2 As Float, Y2 As Float, X3 As Float, Y3 As Float )

Das ist korrekt, denn der aktuelle Punkt wird stets als Anfangspunkt P0(X0|Y0) = A aufgefasst. Somit werden nur die Koordinaten der Punkte B, C und D im CurveTo-Methoden-Aufruf angegeben.

Das ist der vollständige Quelltext, um das Bild in der → Abbildung 23.3.5.3.1 zu zeichnen:

[1] Public Sub PaintScriptBézier4Points()
[2]   Dim vP As Vector
[3]   
[4]   GenerateNewPicture()
[5]   SetPictureBorder()  
[6]   Paint.Begin(hPicture) 
[7]     Paint.Translate(xTranslate, yTranslate)
[8]     Paint.Scale(xScale, yScale) ' +y ▲  
[9]     DrawCoordinateSystem()
[10]      
[11]   ' Vektor mit 8 Elementen, Datentyp: reelle Zahlen (keine komplexen Zahlen)       
[12]     vP = New Vector(8, False)
[13]   ' A(30|30), B(150|250), C(400|60), D(510|210)  
[14]     vP = [30, 30, 150, 250, 400, 60, 510, 210]
[15]     Paint.Brush = Paint.Color(Color.Red)
[16]     Paint.LineWidth = 4
[17]     Paint.LineCap = Paint.LineCapRound
[18] 
[19]     Paint.MoveTo(vP[0], vP[1])    
[20]     Paint.CurveTo(vP[2], vP[3], vP[4], vP[5], vP[6], vP[7])
[21]     Paint.Stroke
[22]     
[23]   ' Verbindungslinien zeichnen A-B-C-D
[24]     Paint.Brush = Paint.Color(Color.Blue)
[25]     Paint.LineWidth = 1
[26]     Paint.Dash = [1, 1] ' Punktierte Linie (ein)
[27]     Paint.MoveTo(vP[0], vP[1])
[28]     Paint.LineTo(vP[2], vP[3])
[29]     Paint.LineTo(vP[4], vP[5])
[30]     Paint.LineTo(vP[6], vP[7])
[31]     Paint.Stroke
[32]     Paint.Dash = [] ' Punktierte Linie (aus)
[33]  
[34]   ' Punkte A,B,C und D einzeichnen
[35]     Paint.Arc(vP[0], vP[1], 3)
[36]     Paint.Arc(vP[2], vP[3], 3)
[37]     Paint.Arc(vP[4], vP[5], 3)
[38]     Paint.Arc(vP[6], vP[7], 3)
[39]     Paint.Fill
[40]     
[41]   ' TEXTE zeichnen 
[42]     Paint.NewPath
[43]     Paint.Scale(1, -1)
[44]     Paint.Font = Font["Monospace, 11"]
[45]     Paint.Brush = Paint.Color(Color.DarkBlue)
[46]     Paint.DrawText("A", 25, -10)
[47]     Paint.DrawText("B", 145, -265)     
[48]     Paint.DrawText("C", 398, -35)
[49]     Paint.DrawText("D", 505, -225)
[50]     Paint.Scale(1, -1)    
[51]   Paint.End
[52]   
[53] End ' PaintScriptBézier4Points()

Kommentar:

• Die ausführlichen Beschreibungen der Prozeduren in den Zeilen 4 und 5 sowie in den Zeilen 7 bis 9 finden Sie im → Kapitel 23.3.3 'Zeichnen mit Paint'.
• In der Zeile 12 wird ein Vektor mit acht Elementen angelegt, deren Datentyp nur reelle Zahlen sind. Die acht Elemente nehmen die x- und y-Koordinaten der 4 Punkt A, B, C und D auf. Die Reihenfolge entspricht der Rangfolge ABCD. Im dritten Beispiel wird eine alternative Angabe der Koordinaten der vier Punkte vorgestellt.
• Über die Anweisungen in den Zeilen 19 bis 21 wird die Bézier-Kurve 3. Grades – definiert durch die 4 Punkte A, B, C und D – in das Koordinatensystem eingezeichnet. Zuerst wird der Anfangspunkt festgelegt und dann die Bézier-Kurve vom Anfangspunkt A zum Endpunkt D in rot nachgezeichnet.

Achtung: Nur zur Verdeutlichung der Lage aller Punkte in Bezug auf die Bézier-Kurve werden in den Anweisungen ab Zeile 23 bestimmte Verbindungslinien und die Stützpunkte B und C eingezeichnet. Die Punkte A, B, C und D werden dabei als Kreis mit sehr kleinem Radius gezeichnet. Abschließend werden die vier Punkte noch bezeichnet – jedoch ohne die Angabe von Koordinaten.

Beispiel 2

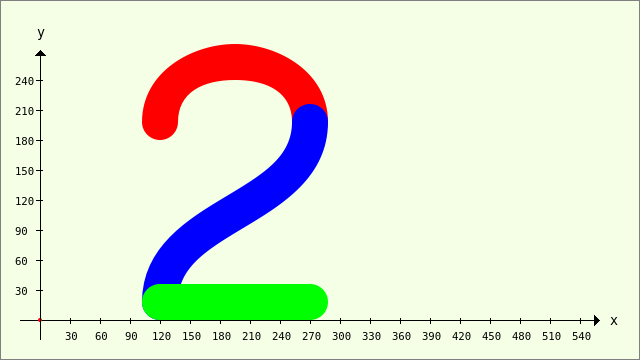
In diesem Beispiel wird eine Zahl 2 aus drei Bézier-Kurven gezeichnet – aus zwei Bézier-Kurven 3. Grades und einer Strecke (Bézier-Kurven ersten Grades).

Abbildung 23.3.5.3.2: Zahl 2 aus drei Bézier-Kurven

Der Quelltext für die Prozedur PaintScriptBezierNumber2() wird vollständig angegeben und kommentiert:

[1] Public Sub PaintScriptBezierNumber2()
[2]   Dim PS, P1, P2, PE As New PointF
[3]   Dim vP, vQ As Vector
[4]   Dim fYOffset As Float
[5]   
[6]   GenerateNewPicture()
[7]   SetPictureBorder()  
[8]   Paint.Begin(hPicture) 
[9]     Paint.Translate(xTranslate, yTranslate)
[10]     Paint.Scale(xScale, yScale) ' +y ▲  
[11]     DrawCoordinateSystem()
[12]   
[13]   ' Ziffer 2 zeichnen
[14]     Paint.Scale(2, 2) ' +Zoom mit dem Faktor 2
[15]     Paint.LineWidth = 18
[16]     fYOffset = Paint.LineWidth / 2
[17]   ' -----------------------------------------------------
[18]   ' Oberer Bogen - rot
[19]     PS.x = 60
[20]     PS.y = 90 + fYOffset
[21]     P1.x = 60
[22]     P1.y = 130 + fYOffset
[23]     P2.x = 135
[24]     P2.y = 130 + fYOffset
[25]     PE.x = 135
[26]     PE.y = 90 + fYOffset
[27]     Paint.LineCap = Paint.LineCapRound
[28]     Paint.Brush = Paint.Color(Color.Red)
[29]     Paint.MoveTo(PS.x, PS.y)
[30]     Paint.CurveTo(P1.x, P1.y, P2.x, P2.y, PE.x, PE.y)
[31]     Paint.Stroke
[32]   ' -----------------------------------------------------    
[33]   ' Mittel-Kurve - blau
[34]     vP = New Vector
[35]     vP = [60, 0, 60, 45, 135, 45, 135, 90]
[36]     vQ = New Vector
[37]     vQ = [0, 1, 0, 1, 0, 1, 0, 1]
[38]   ' vP = [60, 0 + fYOffset, 60, 45 + fYOffset, 135, 45 + fYOffset, 135, 90 + fYOffset]
[39]     vP = vP + fYOffset * vQ
[40]     Paint.Brush = Paint.Color(Color.Blue)
[41]     Paint.MoveTo(vP[0], vP[1])    
[42]     Paint.CurveTo(vP[2], vP[3], vP[4], vP[5], vP[6], vP[7])
[43]     Paint.Stroke
[44]   ' -----------------------------------------------------   
[45]   ' Untere Kurve - grün - Bezier-Kurve 1. Grades (Gerade)
[46]     Paint.Brush = Paint.Color(Color.Green)
[47]     Paint.MoveTo(60, 0 + fYOffset)
[48]     Paint.LineTo(135, 0 + fYOffset) ' Bezier-Kurve 1. Grades
[49]     Paint.Stroke 
[50]   Paint.End
[51] 
[52] End ' PaintScriptBezierNumber2()

Kommentar:

• In der Zeile 14 wird nur für das Zeichnen der Zahl 2 über die Scale-Methode ein Zoom-Faktor von 2 für beide Koordinatenrichtungen verwendet, weil bei den ersten Festlegungen für die jeweils 3 mal 4 Punkte je Kurven-Abschnitt das Bild zwar korrekt, aber zu klein gezeichnet wurde.
• Mit dem Offset in y-Richtung – in Abhängigkeit von der Liniendicke (Zeile 15) – wird erreicht, dass die Zahl 2 stets auf der x-Achse als Grundlinie steht → Zeilen 17 und 18.
• Für den oberen Bogen der Zahl 2 werden den 4 Punkten PE, P1, P2 und PS die Offset-Werte in den Zeilen 19 bis 26 direkt mit den y-Koordinaten-Werten mitgegeben.
• Die Kappen-Form für die Enden der zu zeichnenden Linien wird in der Zeile 27 für alle drei Kurven-Abschnitte vorgeschrieben.
• Das Zeichnen des oberen Kurven-Bogens erfolgt mit den Anweisungen in den Zeilen 29 bis 31.
• Für den mittleren Kurven-Abschnitt wird in der Zeile 34 ein neues Vektor-Objekt angelegt und in der folgenden Zeile über den Inline-Vektor mit 8 Koordinaten für 4 Punkte gefüllt.
• Eine Besonderheit zeigt die Zeile 39. Hier werden zwei Vektoren addiert, wobei der 2. Vektor vQ mit dem Offset multipliziert wird, der aber nur für die Elemente von vQ wirksam wird, die nicht Null sind. Alternativ hätten Sie auch die Zeile 38 verwenden können.
• Der dritte Kurven-Abschnitt ist als Strecke ein Geraden-Abschnitt mit der Krümmung Null und kann als Bézier-Kurve 1. Grades aufgefasst werden → Zeilen 47 und 48.

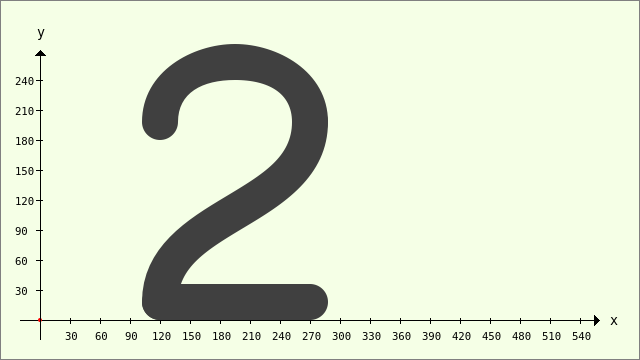
So sieht die Zahl 2 aus, wenn nur eine Farbe zum Zeichnen eingesetzt wird:

Abbildung 23.3.5.3.3: Zahl 2 aus drei Bézier-Kurven

Beispiel 3

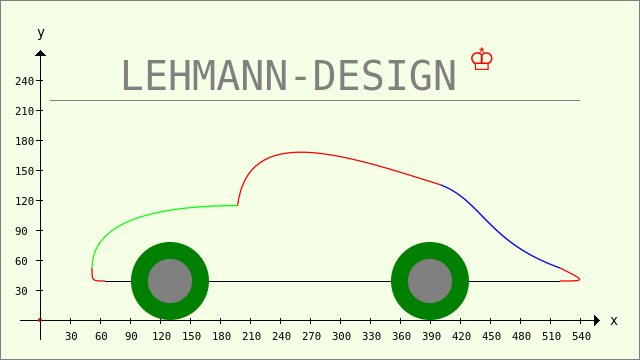
Im diesem Beispiel wird eine Grafik gezeichnet, die aus mehreren Bézier-Kurven 3. Grades und anderen Formen (Strecken, Kreise) besteht. Auf das Zeichnen von Punkten und Verbindungslinien zwischen den Punkten wird verzichtet. Um die einzelnen Kurvenbögen zu unterscheiden, kommen unterschiedliche Farben zum Einsatz. Zusätzlich zu den anderen o.a. Beispielen werden ein Text und ein Symbol eingezeichnet:

Abbildung 23.3.5.3.4: Komplexe Grafik mit Bézier-Kurven

Auch der Quelltext für das dritte Beispiel wird vollständig angegeben und anschließend kommentiert:

[1] Public Sub PaintScriptBezierAuto()
[2]   Dim vP As Vector
[3]   Dim P0, P1, P2, P3 As New PointF
[4]   GenerateNewPicture()
[5]   SetPictureBorder()  
[6]   Paint.Begin(hPicture) 
[7]     Paint.Translate(xTranslate, yTranslate)
[8]     Paint.Scale(xScale, yScale) ' +y ▲  
[9]     DrawCoordinateSystem()
[10]     Paint.Scale(1.3, 1.3) ' +Zoom mit dem Faktor 1.3
[11]     
[12]   ' AUTO
[13]   ' -----------------------------------------------------  
[14]   ' Stoßstange vorn        
[15]     P0 = PointF(50, 30)
[16]     P1 = PointF(40, 30)
[17]     P2 = PointF(40, 30)
[18]     P3 = PointF(40, 40)
[19]     Paint.Brush = Paint.Color(Color.Red)
[20]     Paint.MoveTo(P0.x, P0.y)
[21]     Paint.CurveTo(P1.x, P2.y, P2.x, P2.y, P3.x, P3.y)
[22]     Paint.Stroke
[23]   ' -----------------------------------------------------
[24]   ' Kühlerhaube 
[25]     vP = New Vector
[26]     vP = [40, 40, 40, 80, 100, 88, 152, 88]
[27]     Paint.Brush = Paint.Color(Color.Green)
[28]     Paint.MoveTo(vP[0], vP[1])    
[29]     Paint.CurveTo(vP[2], vP[3], vP[4], vP[5], vP[6], vP[7])
[30]     Paint.Stroke
[31]   ' -----------------------------------------------------    
[32]   ' Frontscheibe und Dach
[33]     vP = New Vector
[34]     vP = [152, 88, 160, 152, 232, 128, 308, 104]
[35]     Paint.Brush = Paint.Color(Color.Red)
[36]     Paint.MoveTo(vP[0], vP[1])    
[37]     Paint.CurveTo(vP[2], vP[3], vP[4], vP[5], vP[6], vP[7])
[38]     Paint.Stroke
[39]   ' -----------------------------------------------------    
[40]   ' Kofferraum-Abdeckung 
[41]     vP = New Vector
[42]     vP = [308, 104, 340, 92, 344, 60, 400, 40]
[43]     Paint.Brush = Paint.Color(Color.Blue)
[44]     Paint.MoveTo(vP[0], vP[1])    
[45]     Paint.CurveTo(vP[2], vP[3], vP[4], vP[5], vP[6], vP[7])
[46]     Paint.Stroke
[47]   ' -----------------------------------------------------    
[48]   ' Stoßstange hinten
[49]     vP = New Vector
[50]     vP = [400, 40, 420, 30, 420, 30, 400, 30]
[51]     Paint.Brush = Paint.Color(Color.Red)
[52]     Paint.MoveTo(vP[0], vP[1])    
[53]     Paint.CurveTo(vP[2], vP[3], vP[4], vP[5], vP[6], vP[7])
[54]     Paint.Stroke
[55]   ' -----------------------------------------------------    
[56]   ' Bodenblech
[57]     Paint.AntiAlias = False      
[58]       Paint.LineWidth = 1
[59]       Paint.Brush = Paint.Color(Color.Black)
[60]       Paint.MoveTo(400, 30)
[61]       Paint.LineTo(50, 30)
[62]       Paint.Stroke
[63]     Paint.AntiAlias = True
[64]   ' Rad vorn
[65]     Paint.Brush = Paint.Color(Color.DarkGreen)    
[66]     Paint.Arc(100, 30, 30)
[67]     Paint.Fill
[68]     Paint.Brush = Paint.Color(Color.Gray)
[69]     Paint.Arc(100, 30, 17)
[70]     Paint.Fill
[71]   ' Rad hinten
[72]     Paint.Brush = Paint.Color(Color.DarkGreen)
[73]     Paint.Arc(300, 30, 30)
[74]     Paint.Fill
[75]     Paint.Brush = Paint.Color(Color.Gray)
[76]     Paint.Arc(300, 30, 17)    
[77]     Paint.Fill  
[78] ' TEXT UND SYMBOL
[79]     Paint.NewPath
[80]     Paint.Scale(1 / 1.3, -1 / 1.3) ' Zoom = 1 und  y-Achse jetzt mit *positiven* Werten nach unten!
[81]     Paint.AntiAlias = False
[82]       Paint.Brush = Paint.Color(Color.Gray)
[83]       Paint.MoveTo(10, -220)
[84]       Paint.LineTo(540, -220)
[85]       Paint.Stroke
[86]     Paint.AntiAlias = True
[87]     Paint.Font = Font["Monospace, 30"]
[88]     Paint.DrawText("LEHMANN-DESIGN", 80, -230) ' Text
[89]     Paint.Font = Font["Monospace, 30, bold"]
[90]     Paint.Brush = Paint.Color(Color.Red)
[91]     Paint.DrawText(String.Chr(9812), 430, -250) ' Symbol Krone
[92]   Paint.End
[93]   
[94] End ' PaintScriptBezierAuto()

Kommentar:

• In der Zeile 10 wird ein Zoom-Faktor von 1,3 zum Zeichen des Autos verwendet, um das Auto mit optimaler Größe zu präsentieren.
• Für die vordere Stoßstange → Zeilen 15 bis 22 werden 4 einzelne Punkte deklariert und ihnen geeignete Koordinatenwerte zugewiesen. Die Anweisung 20 ist notwendig!
• Für alle weiteren Bézier-Kurven wird ein Vektor eingesetzt, der die Koordinaten der 4 Punkte aufnimmt, die Sie zum Zeichnen der Bézier-Kurve benötigen.
• In der Zeile 80 wird der Zoom wieder zurückgenommen und gleichzeitig die y-Achse mit positiver Richtung nach unten (in Bezug auf die Zeichenebene) gesetzt, damit die Schrift nicht spiegelverkehrt angezeigt wird. Achten Sie bei allen Texten auf den negativen y-Wert wegen der Translation in der Zeile 7 mit dem definierten Wert der y-Verschiebung!
• Sie können gern weitere Grafik-Elemente wie Fenster, Türen oder Scheinwerfer ergänzen, denn das Projekt mit allen Beispielen finden Sie im Download-Bereich.