Sidebar
Table of Contents
29.1 Complex numbers
Even if the use of complex numbers is not part of everyday arithmetic with numbers, complex numbers are the first choice for certain applications in electrical engineering or quantum physics. A look at this page http://de.wikipedia.org/wiki/Komplexe_Zahl provides valuable information and basic knowledge.the Complex (gb.complex) class implements complex numbers. The following arithmetic operators and functions are supported in this number range: +, -, *, /, ^, =, <> and Abs(), whereby the absolute value of a complex number is also called the modulus. A complex number represents a pointer in the complex number plane. Perpendicular to the real number line with the unit 1 is the imaginary number line in the centre of the plane. The complex number is usually written as z = a +bi =. Where i is the imaginary unit i, for which i² = -1, a is the real part and b is the imaginary part.
If a real number in Gambas is immediately followed by an “i” or “I”, it is assumed to be a complex number (constant). In this case, the gb.complex component is loaded automatically and adds a new complex class to the interpreter. An 'i' or 'I' alone as a complex number without a real part is recognised as an invalid identifier! Therefore, always write 1i for i. The notation with the capital letter I is obviously specific to Gambas.
29.1.1 Properties
The Complex class has two properties:
| Property | Data type | Description |
|---|---|---|
| Real | Float | Sets or returns the real part of a complex number. |
| Imag | Float | Sets or returns the imaginary part of a complex number. |
Table 29.1.1.1 : Properties of the Complex class
29.1.2 Methods
The Complex class has a static method and several other methods, the description of which can be found in the next table, paying attention to the different return types:
| Method | Return type | Description |
|---|---|---|
| Abs2() | Float | Sets or returns the root of the absolute value of a complex number. |
| Arg() | Float | Returns the argument - in radians - of a complex number. This refers to the angle between the pointer representing the complex number in the number plane and the positive real axis. |
| Conj() | Complex | Returns the conjugate complex number zc to an existing complex number z. |
| Copy() | Complex | Returns a copy of a complex number. |
| Inv() | Complex | Returns the inverse complex number of a complex number. |
| ToString([Local As Boolean ]) | String | Converts a complex number into a string. If the value of the boolean variable Local is TRUE, then the localised number is output; in Germany with the comma as the decimal separator. If the value of the Boolean variable Local is FALSE, a string is returned that can be evaluated with the 'Eval' function. |
Table 29.1.2.1 : Methods of the Complex class
Method Complex.Polar()
The static method Complex.Polar ( [ Abs As Float, Arg As Float ] ) As Complex returns a complex number. The data of the pointer (amount Abs and angle Arg (radian measure) against the positive real axis), which represents the complex number in the complex number plane, are used as arguments.
29.1.3 Generating complex numbers
There are several ways to create complex numbers:
- Using the (static) method Polar( [ Abs As Float, Arg As Float ] ).
- Use of the Conj(), Inv() and Copy() methods. Pay attention to the necessary brackets!
- Use of the Complex( [ Real As Float, Imag As Float ] ) function. Use it to create a new complex number from its real and imaginary parts. If the real or imaginary part is not specified, it is assumed to be zero.
- Conversion of a character string from a suitable (input) component into a complex number.
Example of the use of the Polar(..), Conj(), Inv(), Copy(), Complex(..) and ToString(..) methods:
Dim cZ1, cZ2 As Complex cZ1 = Complex(4, -3) cZ2 = Complex.Polar(4.66, Pi / 3) Print cZ1 + cZ2 ' Sum of 2 complex numbers Z1 and Z2 Print cZ1 - cZ2 ' Difference of 2 complex numbers Z1 and Z2 Print cZ1 * cZ2 ' Product of 2 complex numbers Z1 and Z2 Print cZ1 ^ 3 ' 3rd power of the complex number Z1 Print Abs(cZ1) ' Absolute value of the complex number Z1 Print cZ1.Abs2() ' Square of the absolute value of the complex number Z1 '-- Angle between the pointer of Z1 and the positive real axis (in radians) Print cZ1.Arg() & String.Chr(8596) & Deg(cZ1.Arg() + 2 * Pi) & "°" Print cZ1.Conj() ' Conjugates complex number to Z1 Print cZ1.Copy() ' Copy of the complex number Z1 as a new complex number Print cZ1.Inv() ' Inverse complex number to Z1 Print cZ1.Real ' Real part of complex numbers Z1 Print cZ1.Imag ' Imaginary part of the complex numbers Z1 Print cZ2.ToString(True) ' Conversion from Z2 to a string (localised - comma as decimal separator for DE) Print cZ2.ToString() ' Conversion from Z2 to a string Print Complex(-cZ1.Real,-cZ1.Imag) ' Complex number from the inverted real and imaginary part of Z1
These are the outputs in the console of the Gambas IDE:
[1] 6,33+1,03567838163548i [2] 1,67-7,03567838163548i [3] 21,4270351449065+9,15271352654193i [4] -44-117i [5] 5 [6] 25 [7] -0.64350110879328 ↔ 323.130102354156° [8] 4+3i [9] 4-3i [10] 0,16+0,12i [11] 4 [12] -3 [13] 2,33+4,03567838163548i [14] 2.33+4.03567838163548i [15] -4+3i
29.1.4 Examples
The following examples are tried and tested and provide an initial insight into working with complex numbers. You can find the tried and tested projects in the download area.
29.1.4.1 Example 1 - Solutions of quadratic equations in normal form
A classic example is the calculation of the solutions of a quadratic equation in the general form a-x²+b-x+c = 0. This is first transformed into the normal form x²+p-x+q = 0 in order to make the Vieta test for the two solutions x1 and x2 with x1+x2 = -p and x1-x2 = q simple. You then determine their solution diversity using the discriminant D with D = (p²/4-q) and arrive at exactly 3 distinguishable cases:
1st case: D > 0 → 2 different real solutions or
2nd case: D = 0 → 2 equal real solutions (double solution) or
3rd case: D < 0 → 2 conjugate complex solutions.
Depending on the value of the discriminant D, you must then calculate exactly 2 solutions; either the two real or the two complex solutions. By using the class gb.complex, you can quickly implement the above approach. Here is an excerpt from the source code used:
Public Function Calculate(fP As Float, fQ As Float) As Variant[] Dim fDiskriminante As Float = 0 Dim fX1, fX2 As Float Dim fXC1, fXC2 As Complex fDiskriminante = (fP * fP) / 4 - fQ Select Sgn(fDiskriminante) Case 1 '-- D>0 fX1 = - fP / 2 - Sqr(fDiskriminante) fX2 = - fP / 2 + Sqr(fDiskriminante) Return [fX1, fX2] Case 0 '-- D=0 fX1 = - fP / 2 fX2 = fX1 Return [fX1, fX2] Case Else '-- D<0 fXC1 = Complex(- fP / 2, - Sqr(- fDiskriminante)) fXC2 = fXC1.Conj() Return [fXC1, fXC2] End Select End
Public Sub btnQG_Click() Dim vElement As Variant Dim iCount As Integer = 1 ' Randomize ' For Each vElement In Calculate(Rnd(-2, 2), Rnd(-9, 9)) '-- Random values for the parameters For Each vElement In Calculate(-4, 13) Print "x" & Str(iCount) & " = " & vElement Inc iCount Next ' Alternative: ' Print "x1 = " & Calculate(-4, 13)[0] ' Print "x2 = " & Calculate(-4, 13)[1] End
The solutions of the quadratic equation x²-4-x+13 = 0 are two conjugate complex numbers:
x1 = 2-3i , x2 = 2+3i
29.1.4.2 Example 2 - Use of a custom function IsComplex(..)
For the interactive input of a complex number, you can read a string from a suitable input component - such as a TextBox. Before converting String “ Complex number, it is advantageous to check whether the character string read in matches the pattern a+bi, where a and b are real numbers. You can use the IsComlex(string) function to check whether the character string read in is a complex number a+bi. If successful, you can use the new syntax (→ If sInput MATCH sPattern Then) of the gb.pcre class:
Public Function IsComplex(sInput As String) As Boolean Dim sPattern As String sInput = Trim(sInput) If sInput = "0-0i" Or sInput = "0+0i" Then Return False '-- Dealing with special cases ... sPattern = "^([-+]?[0-9]+(,[0-9]+)?)[-+][0-9]+(,[0-9]+)?[i]$" If sInput Match sPattern Then Return True Else Return False Endif End
It is advantageous if you use an input alphabet as the set of permitted input characters, as it reduces possible incorrect entries:
Public Sub txbInputComplex1_KeyPress() CheckInput("+-,i0123456789") End Public Sub CheckInput(sAllowed As String) ' Idea by Charles Guerin + Benoît Minisini Dim iAllow As Integer = 0 If Key.Code = Key.Left Then iAllow = 1 If Key.Code = Key.Right Then iAllow = 1 If Key.Code = Key.BackSpace Then iAllow = 1 If Key.Code = Key.Delete Then iAllow = 1 If Key.Code = Key.End Then iAllow = 1 If Key.Code = Key.Home Then iAllow = 1 If txbInputComplex1.Text And (Key.Code = Key.Enter Or Key.Code = Key.Return) Then iAllow = 1 If Key.Text And (InStr(sAllowed, Key.Text) > 0) Then iAllow = 1 If iAllow = 0 Then Stop Event End
The conversion String ” Complex number is carried out with the function ValComplex(sInput As String), which returns a complex number as the function value if sInput can be interpreted as a complex number:
Public Function ValComplex(sInput As String) As Complex Dim complexNumber As Complex Dim iCount As Integer Dim sReal, sImaginary As String sInput = Trim(sInput) For iCount = Len(sInput) To 1 Step -1 '-- Inverted iteration If (Mid(sInput, iCount, 1) = "+") Or (Mid(sInput, iCount, 1) = "-") Then sReal = Left(sInput, iCount - 1) sImaginary = Mid(sInput, iCount, Len(sInput) - iCount) complexNumber = Complex(Val(sReal), Val(sImaginary)) Return complexNumber Endif Next End
With the two functions presented, you can check whether a character string read in formally represents a complex number a+bi and then convert the valid character string into a complex number and save it in a suitable variable as required.
29.1.4.3 Example 3 - Calculating with complex numbers
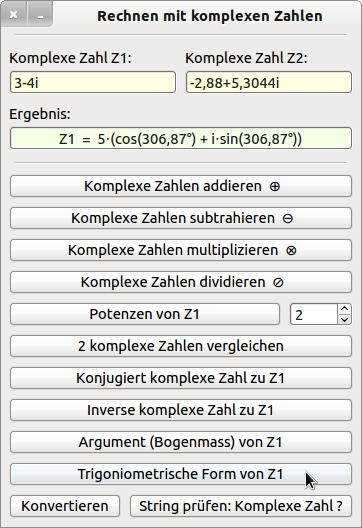
Figure 29.1.4.3.1: Test program for calculating with complex numbers
The following source code excerpt shows you the use of the two functions IsComplex(..) and ValComplex(..) in two variants:
Public Sub btnConvert_Click() If txbInputComplex1.Text Then txbOutputComplex.Clear If IsComplex(txbInputComplex1.Text) = True Then txbOutputComplex.Text = ValComplex(txbInputComplex1.Text).ToString(True) Else Message.Error("The input string cannot be interpreted as a complex number!") txbInputComplex1.SetFocus Endif Endif End
Here is a variant of the above source code snippet in which the IsComplex(..) function is not used. Instead, the Try statement from the Gambas error management is used to catch errors. This is certain to occur if the input string cannot be interpreted as a complex number:
Public Sub btnConvert_Click() If txbInputComplex1.Text Then txbOutputComplex.Clear Try txbOutputComplex.Text = ValComplex(txbInputComplex1.Text).ToString(True) If Error Then Message.Error("The input string cannot be interpreted as a complex number!") txbInputComplex1.SetFocus Endif Endif End
The complete project 'Complex' can be found in the following download area.