GAMBAS-BUCH 3.19.3

Wenn Sie in einem Programm eine ganze Zahl aus einem Intervall [min…max] interaktiv einlesen wollen, dann steht Ihnen dafür auch die Komponente SpinBox zur Verfügung, deren wichtigste Eigenschaften und ihr Einsatz in diesem Kapitel beschrieben werden.

Die Spinbox ist ein Textfeld mit zwei kleinen Tasten (up/down), durch die der aktuelle Wert mit einer frei wählbaren Schrittweite im Intervall [min…max] erhöht oder verringert werden kann. Sie können einen ganzzahligen Wert auch direkt in die Spinbox eingeben. Um diesen Wert zu übernehmen, müssen Sie die Entertaste drücken. Sie können nur Zahlen vom Typ Integer eingeben, weil alle anderen Eingaben – ohne eine Reaktion – nicht akzeptiert werden. Jeder Spinbox können Sie einen definierten Startwert zuweisen. Da alle Werte in einer Spinbox vom Typ Integer sind, müssen Sie für Ihr Programm diese Werte u.U. umrechnen → Exkurs, wenn Sie zum Beispiel das Intervall von [3…10] auf das Intervall [0,0…3,5] abbilden wollen.

Wurde der Maximal- oder Minimalwert erreicht, dann erkennt man das zur Laufzeit am Erscheinungsbild der Spinbox, weil einer der up/down-Tasten grau dargestellt wird. Die SpinBox besitzt für die up/down-Tasten eine Repeat-Funktion.

Der Komponente SpinBox kann man ein Kontext-Menü (PopupMenu) mitgeben, welches dann das Standard-Kontext-Menü der Spinbox ersetzt. Das Menü muss vorher – zum Beispiel im Menüeditor – deklariert werden, damit man das entsprechende Menü im Eigenschaften-Fenster auswählen und der SpinBox zuordnen kann. Alternativ kann man die Zuordnung auch zur Laufzeit des Programms vornehmen. Ausführliche Informationen für diesen Weg erhalten Sie im Kapitel 13.4 'Kontext-Menü'.

Die folgenden Werte (Datentyp Integer) für ausgewählte Eigenschaften einer Spinbox können Sie bereits beim Programmstart zuweisen, sonst werden die Standardwerte gesetzt:

• Minimaler Wert → Standard = 0
• Maximaler Wert → Standard = 100
• Schrittweite → Standard = 1
• Startwert → Standard = 0

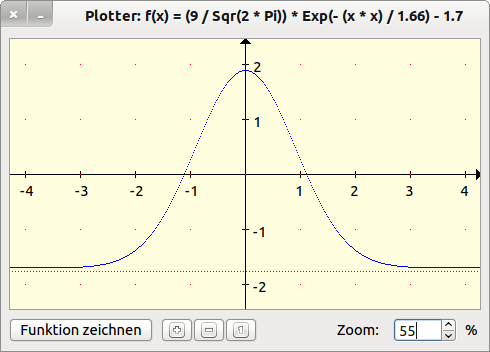
Im folgenden Beispiel wird eine Spinbox eingesetzt, um für das das Bild einer Funktion f(x) den Zoom-Faktor festzulegen. Der Zoom-Faktor ist in einem Bereich von [20%…300%] veränderbar. Die Schrittweite wird auf 5 (%) eingestellt und der Startwert für den Zoom auf 50 (%).

Abbildung 16.12.1: Funktionsplotter mit Zoom-Funktion

Der Quelltext wird nur in den Teilen angegeben, welche die Umsetzung des o.a. Konzepts für eine Zoom-Funktion demonstrieren:

Public Sub Form_Open()
  FMain.Center
  FMain.Resizable = False
  …
  spinboxZoom.MinValue = 20 ' 4 Startwerte
  spinboxZoom.MaxValue = 300
  spinboxZoom.Step = 5
  spinboxZoom.Value = 50
  fZoom = spinboxZoom.Value ' Zoom initialisieren
  spinboxZoom.Tooltip = "Zoom-Bereich 20...300"
' mnu0Einstellungen.Visible = False ' optional
' spinboxZoom.PopupMenu = "mnu0Einstellungen" ' optional
  spinboxZoom.SetFocus
  …
End ' Form_Open
 
Public Sub spinboxZoom_Change()
 
  fZoom = spinboxZoom.Value
  KS_RP_G_Zeichnen(fZoom)
 
End ' spinboxZoom_Change()

In der Prozedur spinboxZoom_Change() der Komponente spinboxZoom wird auf das Change-Ereignis reagiert. Der Variablen fZoom (Datentyp Float) wird dann der aktuelle Wert der Spinbox zugewiesen. Dieser Wert ist Parameterwert der Prozedur KS_RP_G_Zeichnen(fZoom), die das Koordinatensystem, die Rasterpunkte und abschließend den Graphen der gegebenen Funktion f(x) mit dem aktuellen Zoom-Faktor zeichnet.

Die Nutzung der drei Button mit den Beschriftungen +, - und 1 zeigt als optionale Erweiterung einen anderen Weg, um eine Zoom-Funktion zu realisieren, bei der die Spinbox u.a zur Anzeige des aktuellen Zoom-Faktors genutzt wird:

Public Sub btnZoomNormal_Click()
  fZoom = 50 ' Angabe in %
  spinboxZoom.Value = fZoom
  KS_RP_G_Zeichnen(fZoom) ' Koordinatensystem, Rasterpunkte und Graph
End ' btnZoomNormal_Click()
 
Public Sub btnZoomG_Click()
  If fZoom < 300 Then 
     fZoom += 5
     spinboxZoom.Value = fZoom
     KS_RP_G_Zeichnen(fZoom)
  Endif ' fZoom < 300
End ' btnZoomG_Click()
 
Public Sub btnZoomK_Click()
  If fZoom > 20 Then
     fZoom -= 5 
     spinboxZoom.Value = fZoom
     KS_RP_G_Zeichnen(fZoom)
  Endif ' fZoom > 20
End ' btnZoomK_Click()

Den Wert der Eigenschaft Spinbox.Text (Datentyp String) können Sie nur auslesen und sofort zur Anzeige des aktuellen Wertes der Spinbox in einer geeigneten Komponente verwenden.

Exkurs

Um zum Beispiel das Intervall von [3…10] auf das Intervall [0,0…3,5] linear abzubilden, benötigt man die lineare Funktion durch die beiden Punkte P0(3|0] und P1(10|3,5). Der (allgemeine) Ansatz für eine lineare Gleichung (y-y0)·(x1-x0) = (y1-y0)·(x-x0) führt auf k(x) = 0,5·x – 1,5 mit x ∈ N im eingeschränkten Definitionsbereich 3 ≤ x ≤ 10.

Public Function k(x As Integer) As Float
  Return 0.5 * x - 1.5
End ' Function k(x)

Der allgemeine Ansatz, um das Intervall [a…b] auf das Intervall [p…q] abzubilden, führt auf die lineare Gleichung (y-y0)·(x1-x0) = (y1-y0)·(x-x0) → (y-p)·(b-a) = (q-p)·(x-a) mit a ≠ b. Das Umstellen nach y ergibt die allgemeine Gleichung für die Konvertierungsfunktion k(x) mit x ∈ N im eingeschränkten Definitionsbereich a ≤ x ≤ b.