Seitenleiste
Inhaltsverzeichnis
29.1 Komplexe Zahlen
Auch wenn die Verwendung von komplexen Zahlen nicht zum täglichen Rechnen mit Zahlen gehört – für bestimmte Anwendungen aus der Elektrotechnik oder der Quantenphysik sind komplexe Zahlen aber die erste Wahl. Ein Blick auf diese Seite http://de.wikipedia.org/wiki/Komplexe_Zahl liefert wertvolle Informationen und Grundlagenwissen. Die Klasse Complex (gb.complex) implementiert komplexe Zahlen. In diesem Zahlenbereich werden die folgenden arithmetischen Operatoren und Funktionen: +, -, *, /, ^, =, <> und Abs() unterstützt, wobei der Absolutwert einer komplexen Zahl auch Modul genannt wird. Eine komplexe Zahl repräsentiert einen Zeiger in der komplexen Zahlenebene. Senkrecht zum reellen Zahlenstrahl mit der Einheit 1 steht der imaginäre Zahlenstrahl im Zentrum der Ebene. Für die komplexe Zahl ist die Schreibweise z = a +bi = üblich. Dabei sind i die imaginäre Einheit i, für die i² = -1 gilt, a der Realteil und b der Imaginärteil.
Wenn einer reellen Zahl in Gambas unmittelbar ein „i“ oder „I“ folgt, dann wird angenommen, das es sich um eine komplexe Zahl(-Konstante) handelt. In diesem Fall wird die Komponente gb.complex automatisch geladen und fügt eine neue Complex-Klasse zum Interpreter hinzu. Ein 'i' oder 'I' allein als komplexe Zahl ohne Realteil wird als ungültiger Bezeichner erkannt! Schreiben Sie deshalb für i stets 1i. Die Schreibweise mit dem Großbuchstaben I ist offenbar gambas-spezifisch.
29.1.1 Eigenschaften
Die Klasse Complex verfügt über zwei Eigenschaften:
| Eigenschaft | Datentyp | Beschreibung |
|---|---|---|
| Real | Float | Setzt den reellen Teil einer komplexen Zahl oder gibt diesen zurück. |
| Imag | Float | Setzt den imaginären Teil einer komplexen Zahl oder gibt diesen zurück. |
Tabelle 29.1.1.1 : Eigenschaften der Klasse Complex
29.1.2 Methoden
Die Klasse Complex verfügt über eine statische Methode und mehrere weitere Methoden, deren Beschreibung Sie in der nächsten Tabelle finden, wobei auf die unterschiedlichen Rückgabetypen zu achten ist:
| Methode | Rückgabetyp | Beschreibung |
|---|---|---|
| Abs2() | Float | Setzt die Wurzel aus dem Absolutwert einer komplexen Zahl oder gibt diesen zurück. |
| Arg() | Float | Gibt das Argument – im Bogenmaß – einer komplexen Zahl zurück. Gemeint ist der Winkel zwischen dem Zeiger, der die komplexe Zahl in der Zahlenebene repräsentiert und der positiven reellen Achse. |
| Conj() | Complex | Gibt die konjugiert komplexe Zahl zc zu einer vorhandenen komplexen Zahl z zurück. |
| Copy() | Complex | Gibt eine Kopie einer komplexen Zahl zurück. |
| Inv() | Complex | Gibt die inverse komplexe Zahl einer komplexen Zahl zurück. |
| ToString([Local As Boolean ]) | String | Konvertiert eine komplexe Zahl in einen String. Ist der Wert der boolschen Variablen Local gleich TRUE, dann wird die lokalisierte Zahl ausgegeben; in Deutschland mit dem Komma als Dezimal-Trennzeichen. Ist der Wert der boolschen Variablen Local gleich FALSE, dann wird ein String zurückgegeben, der mit der Funktion 'Eval' ausgewertet werden kann. |
Tabelle 29.1.2.1 : Methoden der Klasse Complex
Methode Complex.Polar()
Die statische Methode Complex.Polar ( [ Abs As Float, Arg As Float ] ) As Complex gibt eine komplexe Zahl zurück. Als Argumente werden die Daten des Zeigers (Betrag Abs und Winkel Arg (Bogenmaß) gegen die positive reelle Achse) eingesetzt, der die komplexe Zahl in der komplexen Zahlenebene repräsentiert.
29.1.3 Erzeugen komplexer Zahlen
Es gibt mehrere Möglichkeiten komplexe Zahlen zu erzeugen:
- Einsatz der (statischen) Methode Polar( [ Abs As Float, Arg As Float ] ).
- Verwendung der Methoden Conj(), Inv() und Copy(). Achten Sie auf die notwendigen Klammern!
- Einsatz der Funktion Complex( [ Real As Float, Imag As Float ] ). Erstellen Sie damit eine neue komplexe Zahl aus seinem Real- und Imaginär-Teil. Wenn der Real- oder Imaginär-Teil nicht angegeben ist, dann wird angenommen, das dieser Null ist.
- Konvertierung einer Zeichenkette aus einer geeigneten (Eingabe-)Komponente in eine komplexe Zahl.
Beispiel für die Nutzung der Methoden Polar(..), Conj(), Inv(), Copy(), Complex(..) und ToString(..):
Dim cZ1, cZ2 As Complex cZ1 = Complex(4, -3) cZ2 = Complex.Polar(4.66, Pi / 3) Print cZ1 + cZ2 ' Summe von 2 komplexen Zahlen Z1 und Z2 Print cZ1 - cZ2 ' Differenz von 2 komplexen Zahlen Z1 und Z2 Print cZ1 * cZ2 ' Produkt von 2 komplexen Zahlen Z1 und Z2 Print cZ1 ^ 3 ' 3. Potenz der komplexen Zahl Z1 Print Abs(cZ1) ' Betrag der komplexen Zahl Z1 Print cZ1.Abs2() ' Quadrat des Betrages der komplexen Zahl Z1 'Winkel zwischen Zeiger von Z1 und der positiven reellen Achse (im Bogenmaß) Print cZ1.Arg() & String.Chr(8596) & Deg(cZ1.Arg() + 2 * Pi) & "°" Print cZ1.Conj() ' Konjugiert komplexe Zahl zu Z1 Print cZ1.Copy() ' Kopie der komplexen Zahl Z1 als neue komplexe Zahl Print cZ1.Inv() ' Inverse komplexe Zahl zu Z1 Print cZ1.Real ' Real-Teil der komplexen Zahlen Z1 Print cZ1.Imag ' Imaginär-Teil der komplexen Zahlen Z1 Print cZ2.ToString(True) ' Konvertierung Z2 in einen String (lokalisiert – Komma als Dezimaltrennzeichen) Print cZ2.ToString() ' Konvertierung Z2 in einen String Print Complex(-cZ1.Real,-cZ1.Imag) ' Komplexe Zahl aus dem invertierten Real- und Imaginär-Teil von Z1
Das sind die Ausgaben in der Konsole der Gambas-IDE:
[1] 6,33+1,03567838163548i [2] 1,67-7,03567838163548i [3] 21,4270351449065+9,15271352654193i [4] -44-117i [5] 5 [6] 25 [7] -0.64350110879328 ↔ 323.130102354156° [8] 4+3i [9] 4-3i [10] 0,16+0,12i [11] 4 [12] -3 [13] 2,33+4,03567838163548i [14] 2.33+4.03567838163548i [15] -4+3i
29.1.4 Beispiele
Die folgenden Beispiele sind erprobt und gewähren einen ersten Einblick in die Arbeit mit komplexen Zahlen. Im Download-Bereich finden Sie die erprobten Projekte. 29.1.4.1 Beispiel 1 – Lösungen von quadratischen Gleichungen in der Normalform Ein klassisches Beispiel ist die Berechnung der Lösungen einer quadratischen Gleichung in der allgemeinen Form a·x²+b·x+c = 0. Diese wird zuerst in die Normalform x²+p·x+q = 0 transformiert, um die Probe nach Vieta für die beiden Lösungen x1 und x2 mit x1+x2 = -p und x1·x2 = q einfach zu gestalten. Danach bestimmen Sie deren Lösungsvielfalt mit Hilfe der Diskriminante D mit D = (p²/4-q) und kommen auf genau 3 unterscheidbare Fälle:
1. Fall: D > 0 → 2 verschiedene reelle Lösungen oder
2. Fall: D = 0 → 2 gleiche reelle Lösungen (Doppel-Lösung) oder
3. Fall: D < 0 → 2 konjugiert komplexe Lösungen.
Anschließend müssen Sie – je nach Wert der Diskriminante D – jeweils genau 2 Lösungen berechnen; entweder die zwei reellen oder die zwei komplexen. Mit dem Einsatz der Klasse gb.complex können Sie den o.a. Ansatz schnell umsetzen. Hier ein Auszug aus dem verwendeten Quelltext:
Public Function Calculate(fP As Float, fQ As Float) As Variant[] Dim fDiskriminante As Float = 0 Dim fX1, fX2 As Float Dim fXC1, fXC2 As Complex fDiskriminante = (fP * fP) / 4 - fQ Select Sgn(fDiskriminante) Case 1 ' D>0 fX1 = - fP / 2 - Sqr(fDiskriminante) fX2 = - fP / 2 + Sqr(fDiskriminante) Return [fX1, fX2] Case 0 ' D=0 fX1 = - fP / 2 fX2 = fX1 Return [fX1, fX2] Case Else ' D<0 fXC1 = Complex(- fP / 2, - Sqr(- fDiskriminante)) fXC2 = fXC1.Conj() Return [fXC1, fXC2] End Select End ' Calculate(fP As Float, fQ As Float) As Variant[]
Public Sub btnQG_Click() Dim vElement As Variant Dim iCount As Integer = 1 ' Randomize ' For Each vElement In Calculate(Rnd(-2, 2), Rnd(-9, 9)) ' Zufallswerte für die Parameter For Each vElement In Calculate(-4, 13) Print "x" & Str(iCount) & " = " & vElement Inc iCount Next ' vElement ' Alternative: ' Print "x1 = " & Calculate(-4, 13)[0] ' Print "x2 = " & Calculate(-4, 13)[1] End ' btnQG_Click()
Die Lösungen der quadratischen Gleichung x²-4·x+13 = 0 sind zwei konjugiert komplexen Zahlen:
x1 = 2-3i , x2 = 2+3i
29.1.4.2 Beispiel 2 – Einsatz einer eigenen Funktion IsComplex(..)
Für die interaktive Eingabe einer komplexen Zahl können Sie einen String aus einer geeigneten Eingabe-Komponente – wie zum Beispiel einer TextBox – auslesen. Es ist vorteilhaft, vor der Konvertierung String « Komplexe Zahl zu prüfen, ob die eingelesene Zeichenkette auf das Muster a+bi passt, wobei a und b reelle Zahlen sind. Mit der Funktion IsComlex(string) können Sie prüfen, ob es sich bei der eingelesenen Zeichenkette um eine komplexe Zahl a+bi handelt. Mit Erfolg können Sie die neue Syntax (→ If sInput MATCH sPattern Then) der Klasse gb.pcre einsetzen:
Public Function IsComplex(sInput As String) As Boolean Dim sPattern As String sInput = Trim(sInput) If sInput = "0-0i" Or sInput = "0+0i" Then Return False ' Sonderfälle behandeln ... sPattern = "^([-+]?[0-9]+(,[0-9]+)?)[-+][0-9]+(,[0-9]+)?[i]$" If sInput Match sPattern Then Return True Else Return False Endif ' Match Pattern End ' Function IsComplex(sInput As String) As Boolean
Es ist von Vorteil, wenn Sie ein Eingabe-Alphabet als Menge der zulässigen Eingabe-Zeichen verwenden, denn es reduziert mögliche Fehleingaben:
Public Sub txbInputComplex1_KeyPress() CheckInput("+-,i0123456789") End ' txbInputComplex_KeyPress() Public Sub CheckInput(sAllowed As String) ' Idee von Charles Guerin + Benoît Minisini Dim iAllow As Integer = 0 If Key.Code = Key.Left Then iAllow = 1 If Key.Code = Key.Right Then iAllow = 1 If Key.Code = Key.BackSpace Then iAllow = 1 If Key.Code = Key.Delete Then iAllow = 1 If Key.Code = Key.End Then iAllow = 1 If Key.Code = Key.Home Then iAllow = 1 If txbInputComplex1.Text And (Key.Code = Key.Enter Or Key.Code = Key.Return) Then iAllow = 1 Endif If Key.Text And (InStr(sAllowed, Key.Text) > 0) Then iAllow = 1 If iAllow = 0 Then Stop Event End ' CheckInput(sAllowed As String)
Die Konvertierung String « Komplexe Zahl erfolgt mit der Funktion ValComplex(sInput As String), die als Funktionswert eine komplexe Zahl liefert, wenn sInput als komplexe Zahl interpretiert werden kann:
Public Function ValComplex(sInput As String) As Complex Dim complexNumber As Complex Dim iCount As Integer Dim sReal, sImaginary As String sInput = Trim(sInput) For iCount = Len(sInput) To 1 Step -1 ' Invertierte Iteration If (Mid(sInput, iCount, 1) = "+") Or (Mid(sInput, iCount, 1) = "-") Then sReal = Left(sInput, iCount - 1) sImaginary = Mid(sInput, iCount, Len(sInput) - iCount) complexNumber = Complex(Val(sReal), Val(sImaginary)) Return complexNumber Endif ' + oder - ? Next ' iCount End ' Function ValComplex(sInput As String) As Complex
Mit den beiden vorgestellten Funktionen können Sie prüfen, ob eine eingelesene Zeichenkette formal eine komplexe Zahl a+bi repräsentiert und anschließend die valide Zeichenkette in eine komplexe Zahl konvertieren und nach Bedarf in einer geeigneten Variablen speichern.
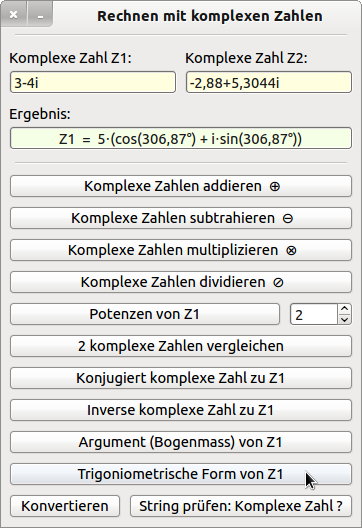
29.1.4.3 Beispiel 3 – Rechnen mit komplexen Zahlen
Abbildung 29.1.4.3.1: Test-Programm zum Rechnen mit komplexen Zahlen
Der folgende Quelltext-Ausschnitt zeigt Ihnen den Einsatz der beiden vorgestellten Funktionen IsComplex(..) und ValComplex(..) in zwei Varianten:
Public Sub btnConvert_Click() If txbInputComplex1.Text Then txbOutputComplex.Clear If IsComplex(txbInputComplex1.Text) = True Then txbOutputComplex.Text = ValComplex(txbInputComplex1.Text).ToString(True) Else Message.Error("Der Eingabe-String kann\nnicht\nals komplexe Zahl interpretiert werden!") txbInputComplex1.SetFocus Endif ' IsComplex(..) ? Endif ' txbInputComplex.Text End ' btnConvert_Click()
Hier eine Variante zum o.a. Quelltext-Ausschnitt, in der die Funktion IsComplex(..) nicht genutzt wird. Dafür kommt die Try-Anweisung aus dem Fehler-Management von Gambas zum Einsatz, um Fehler abzufangen. Der tritt mit Sicherheit genau dann auf, wenn der Eingabe-String nicht als komplexe Zahl interpretiert werden kann:
Public Sub btnConvert_Click() If txbInputComplex1.Text Then txbOutputComplex.Clear Try txbOutputComplex.Text = ValComplex(txbInputComplex1.Text).ToString(True) If Error Then Message.Error("Der Eingabe-String kann\nnicht\nals komplexe Zahl interpretiert werden!") txbInputComplex1.SetFocus Endif ' ERROR ? Endif ' txbInputComplex.Text End ' btnConvert_Click()
Das vollständige Projekt Complex finden Sie im Download-Bereich.