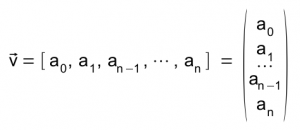Seitenleiste
Inhaltsverzeichnis
29.3.5 Vector
Die Klasse Vector aus der Komponente gb.gsl implementiert einen Vektor mit reellen oder komplexen Koordinaten oder Komponenten. Ein Vektor kann wie ein Lese-/Schreib-Array verwendet werden. Die Klasse Vector verfügt über zwei Eigenschaften und fünf Methoden.
29.3.5.1 Vektor-Begriff
Ein Vektor kann als Zeilen- oder Spalten-Vektor so dargestellt werden:
- Ein Vektor ist ein spezieller n-Tupel. Unter einem Tupel versteht man eine endliche Liste aus n mathematischen Objekten aus unterschiedlichen mathematischen Objekt-Klassen.
- Für die Klasse Vector in Gambas sind die mathematischen Objektklassen entweder reelle oder komplexe Zahlen. Werden komplexe Zahlen eingesetzt, dann ist das explizit anzugeben.
- Die reellen oder komplexen Zahlen ai in einem Zeilen- oder Spalten-Vektor nennt man Koordinaten oder Komponenten.
- Den Betrag oder die Länge eines Vektors bezeichnet man als seine (euklidische) Norm.
29.3.5.2 Eigenschaften
Die Klasse Vector hat zwei Eigenschaften:
| Eigenschaft | Datentyp | Beschreibung |
|---|---|---|
| Count | Integer | Gibt die Anzahl der Koordinaten oder Komponenten eines Vektors zurück. |
| Handle | Zeiger | Gibt einen Zeiger (Pointer) auf das interne GSL-Vektor-Objekt zurück. |
Tabelle 29.3.5.2.1 : Eigenschaften der Klasse Vector
29.3.5.3 Methoden
Die Klasse Vector besitzt diese fünf Methoden:
| Methode | Rückgabetyp | Beschreibung |
|---|---|---|
| ConjDot ( Vector As Vector ) | Variant | Zurückgegeben wird das komplexe konjugierte Skalar-Produkt zwischen dem aktuellen Vektor und einem weiteren Vektor. |
| Copy ( ) | Vector | Zurückgegeben wird eine Kopie des Vektors. |
| Dot ( Vector As Vector ) | Variant | Zurückgegeben wird das Skalar-Produkt zwischen dem aktuellen Vektor und einem weiteren Vektor. |
| Norm ( ) | Float | Es wird der Betrag oder die Länge eines Vektors zurückgegeben. |
| ToString ([ Local As Boolean ]) | String | Zurückgegeben wird der Vektor als String-Repräsentation – in Abhängigkeit vom Parameter 'Local'. |
Tabelle 29.3.5.3.1 : Methoden der Klasse Vector
Hinweis:
- Die Kopie eines Vektors ist ein eigenständiges Vektor-Objekt.
- Hat der Parameter Local den Wert True werden Zahlen in der lokalen Notation ausgegeben, während der Standard-Wert False den String so formatiert, dass er von der Funktion Eval(..) ausgewertet werden kann.
29.3.5.4 Erzeugen von Vektoren
Es gibt unterschiedliche Möglichkeiten um Vektoren zu erzeugen:
(A) Deklaration einer Variablen vom Daten-Typ Vector mit direkter Wertzuweisung.
(B) Deklaration einer Variablen vom Daten-Typ Vector und spätere Zuweisung der Koordinaten in einem Array.
(C) Kopie eines Vektors anlegen.
(D) Konvertierung einer Zeichenkette aus einer geeigneten (Eingabe-)Komponente in einen Vektor als Teil-Quelltext in einem Projekt.
Beispiel A
Public voA As New Vector(3, False)
Beispiel B
Dim voD As Vector voD = New Vector(4, False) voD = [-3.4, 5, -6, 2] ' Print voD.ToString(True)
Beispiel C
Dim voA, voB As Vector voA = New Vector(3, False) voA = [5, -6, 2] voB = voA.Copy() ' Print voB.ToString(True)
29.3.5.5 Operationen und Relationen
Für Vektoren sind u.a. die folgenden Operationen erklärt:
- Addition, Subtraktion und die skalare Multiplikation (Skalar-Produkt).
- Als Relationen zwischen 2 Vektoren existieren der direkte Vergleich und die Prüfung auf Ungleichheit.
Dim voA, voB, voC As Vector voA = [1, 1, 2] voB = [5, -4, 3] voC = [3, 6, 7] Print "Ortsvektor OA: "; voA.ToString(True) Print "Ortsvektor OB: "; voB.ToString(True) Print "Ortsvektor OC: "; voC.ToString(True) Print "-----------------------------------------" Print "Vektor-Summe: OA+OB = " & (voA + vob).ToString(True) Print "Vektor-Differenz: OA-OB = " & (voA - voB).ToString(True) Print "Skalar-Produkt: OA" & String.Chr(&H22C5) & "OB = z = "; voA.Dot(voB) Print "Vergleich: OA ungleich Kopie von OB? » "; voA <> voB.Copy() Print "Vergleich: OC gleich OB? » "; voc = voB
In der IDE-Konsole lesen Sie:
Ortsvektor OA: [1 1 2] Ortsvektor OB: [5 -4 3] Ortsvektor OC: [3 6 7] ----------------------------------------- Vektor-Summe: OA+OB = [6 -3 5] Vektor-Differenz: OA-OB = [-4 5 -1] Skalar-Produkt: OA⋅OB = z = 7 Vergleich: OA ungleich Kopie von OB? » True Vergleich: OC gleich OB? » False
29.3.5.6 Projekt
Das folgende Projekt setzt die vierte Variante (D) zur Erzeugung eines Vektors über die Konvertierung einer Zeichenkette aus einer geeigneten (Eingabe-)Komponente um.
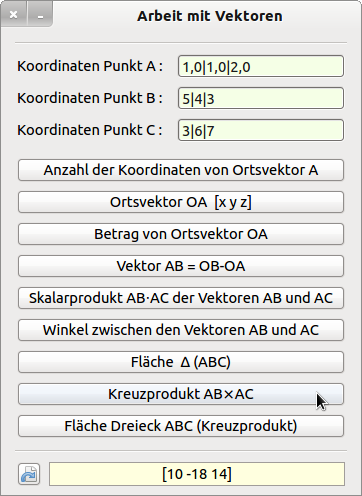
- Vorgabe: Die drei Vektoren sind Ortsvektoren in einem kartesischen Koordinatensystem.
- Die Koordinaten der Vektoren werden im Format: x|y|z in eine Textbox – x, y und z sind reelle Zahlen – eingegeben (→ Abbildung 29.3.5.6.1) und aus dem formatierten String ausgelesen.
- Für die drei Textboxen wird ein Eingabe-Alphabet vorgegeben und übergeprüft, so dass Fehleingaben erheblich reduziert werden (→ CheckInput(..) und TBGroup_KeyPress()).
- Geprüft wird in einer Konvertierungsfunktion Convert2Vektor(..) u.a. mit einem regulären Ausdruck, ob jeweils nur valide Eingaben in den drei Text-Boxen gemacht wurden. Trifft das zu, wird die Zeichenkette zerlegt und in einen Vektor konvertiert.
Public Sub Form_Open() ... ' Dezimaltrennzeichen nach Locale setzen If Left$(Format$(0, ".0")) = "," Then txbInputA.Text = "1,0|1,0|2,0" Else txbInputA.Text = "1.0|1.0|2.0" Endif End ' Form_Open() Public Sub CheckInput(sAllowed As String) ' Idee: Charles Guerin Select Case Key.Code Case Key.Left, Key.Right, Key.BackSpace, Key.Delete, Key.End, Key.Home, Key.Enter, Key.Return Return Default If Key.Text And If InStr(sAllowed, Key.Text) Then Return Endif End Select Stop Event End ' CheckInput(sAllowed As String) Public Sub TBGroup_KeyPress() ' Gilt für die *TextBox-Gruppe* TBGroup aus 3 Textboxen! If Left$(Format$(0, ".0")) = "," Then CheckInput("+-,|0123456789") Else CheckInput("+-.|0123456789") Endif End ' TBGroup_KeyPress() Public Function Convert2Vector(sInput As String) As Vector ' Eingabe-String → Vektor Dim sSubject, sPattern As String Dim vVector As Vector Dim aArray As String[] sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Match sPattern Then aArray = Split(sInput, "|") vVector = [Val(aArray[0]), Val(aArray[1]), Val(aArray[2])] Return vVector Else Return Error.Raise("Eingabefehler Koordinaten") Endif End ' Convert2Vector(..)
Im Projekt werden fast alle Eigenschaften und Methoden der Klasse Vector eingesetzt. Die drei Ortsvektoren legen ein Dreieck im Raum fest, von dem einige Eigenschaften berechnet werden.
Abbildung 29.3.5.6.1: Demonstration der Arbeit mit Vektoren
Mit der Funktion IsVector(txbInputA.Text) können Sie zum Beispiel prüfen, ob die aus einer Textbox für den Punkt A ausgelesene Zeichenkette als Punkt in einem kartesischen Koordinatensystem interpretiert werden kann.
Die o.a. Funktion wird im Projekt nicht verwendet. Es wird aber das gleiche Suchmuster in einem regulären Ausdruck wie bei der Funktion Convert2Vector(..) verwendet.
Private Function IsVector(sInput As String) As Boolean Dim sSubject, sPattern As String sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Not Match sPattern Then Return False Return True End ' IsVector(sInput As String) As Boolean
Die Berechnung des Kreuzproduktes V1✘V2 zweier Vektoren wird durch diese Funktion realisiert:
Public Function SetAxB(vV1 As Vector, vV2 As Vector) As Vector ' Kreuzprodukt vV1✘vV2 Dim fx, fy, fz As Float fx = vV1[1] * vV2[2] - vV2[1] * vV1[2] fy = vV1[0] * vV2[2] - vV2[0] * vV1[2] fz = vV1[0] * vV2[1] - vV2[0] * vV1[1] Return [fx, - fy, fz] End ' Function SetAxB(vV1, vV2)
Den vollständigen, hinreichend kommentierten Quelltext finden Sie im Download-Bereich.