GAMBAS-BUCH 3.19.5

Bei einem Projekt „Funktionsplotter“ tauchten Probleme an einer Stelle auf, die so vorher nicht im Blickpunkt standen. Während die Darstellung einer im Quelltext fest codierten Funktion y = f(x)

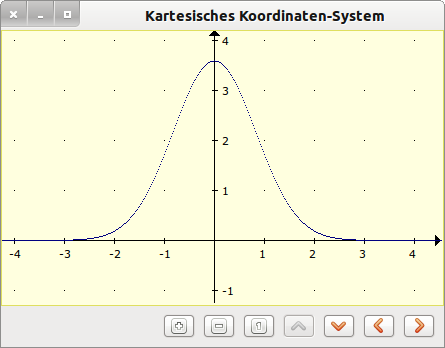
Public Function f(x As Float) As Float ' Das Argument ist x
  RETURN (9 / Sqr(2 * pi)) * Exp(- (x * x) / 1.66)
End ' Function f(..)

mit Zoom und Verschiebung gut funktionierte, erwiesen sich die interaktive Eingabe der zu zeichnenden Funktion und die Berechnung der Funktionswerte als Problem, um den Funktionsplotter universell nutzen zu können!

Abbildung 19.8.1.1: Dichtefunktion (Normalverteilung)

Erste erfolgversprechende Ansätze ergaben sich im Zusammenhang mit der direkten Auswertung von (Gambas-)Ausdrücken. Hinweise und Beispiele zur Auswertung von (Gambas-)Ausdrücken finden Sie im Kapitel 25.5.3.

In der Gambas-Hilfe zum Interpreter steht:

Wenn Sie den Gambas-Interpreter gbx3 in einem Terminal mit der Option -e aufrufen, dann können Sie einen als Parameter übergebenen <Ausdruck> auswerten und sich das Ergebnis anzeigen lassen:

Verwendung:		gbx3 -e <Ausdruck> 
Option: 		-e   einen Ausdruck auswerten 

Hier folgt ein erprobtes Beispiel:

hans@linux:~$ gbx3 -e "2.44-sin(pi/3)" 
1,57397459621556 

Dabei steht die Option -e für die Verwendung der Funktion Eval(..) . Wenn Sie diese Funktion aufrufen, wird die Komponente gb.eval automatisch geladen:

Value = Eval ( Expression AS String [ , Context AS Collection ] ) AS Variant 

Der Text in der Gambas-Hilfe stützt diese Auffassung:

Eval(..) wertet einen Ausdruck aus und gibt seinen Wert zurück. Dieser Ausdruck kann fast alle Operatoren und Unterprogramme von Gambas enthalten. Der optionale Kontext ist eine Collection, die den Wert der einzelnen nicht definierten Symbole enthalten muss.

Am Interessantesten ist jedoch der letzte Satz! Wenn Sie sich die Zuordnungsvorschrift in einer weiteren Funktion y = g(x) = e*sin(x) + x^3 - cbr(x) - pi genau ansehen, dann enthält der algebraische Ausdruck auch die in Gambas bekannten Funktionen sin(x), Potenzfunktion x^3 und die Wurzel-Funktion cbr(x) mit dem Wurzelexponenten (1/3). Auch das Symbol Pi ist bekannt! Der Parameter e als Eulersche Zahl und die Variable x sind offensichtlich die o.a. nicht definierten Symbole. Diese gilt es p.d. über den Context festzulegen. Damit entsteht folgender erster Lösungsansatz für die Berechnung der Wertetabelle für die Funktion g(x). Mit deren Wertepaaren kann später das Bild der Funktion im Projekt „Funktionsplotter“ iterativ gezeichnet werden.

Der folgende Quelltext gehört zu einem Test-Projekt, das den Nachweis lieferte, eine interaktiven Eingabe einer Funktion zu realisieren und die Funktion Evel() erfolgreich zur Berechnung von Funktionswerten einzusetzen. Hier der vollständige und hinreichend kommentierte Quelltext:

' Gambas class file 
 
Public Sub Form_Open() 
  FMain.Center 
  FMain.Resizable = False 
  txbFunction.Text = "e*Sin(x) + x^3 - Cbr(x) - Pi" ' Default-Function
End ' Form_Open() 
 
Public Sub btnComputeTOV_Click() ' TOV → TableOfValues
  Dim y As Float 
  Dim Context As New Collection 
 
  txaTableOfValues.Clear 
  Context["e"] = Exp(1) ' Dem Symbol e wird der Wert e=Exp(1) (= e^1)zugewiesen 
  Context["x"] = -3     ' Dem Symbol x wird der Wert -3 zugewiesen 
 
  Repeat 
    Try y = Eval(txbFunction.Text, Context) ' Interaktive Eingabe von f(x) in txbFunction.Text
    If Error Then 
       Message.Error("Das ging in die Hose...!") 
       Return 
    Endif ' ERROR 
    txaTableOfValues.Insert(gb.Tab & Round(CFloat(Context["x"]), -3) & gb.Tab & "         " \
                            & Round(CFloat(y), -4) & gb.NewLine) 
    Context["x"] = Context["x"] + 0.01 ' Dem Symbol x wird ein erhöhter Wert zugewiesen 
  Until Context["x"] > 3.001 ' Abbruch, wenn das Symbol x einen Wert > 3.001 hat 
 
End ' btnComputeTOV_Click() 
 
Public Sub txbFunction_Change() 
  txaTableOfValues.Clear 
End ' txbFunction_Change() 
 
Public Sub btnClose_Click() 
  FMain.Close 
End ' btnClose_Click() 

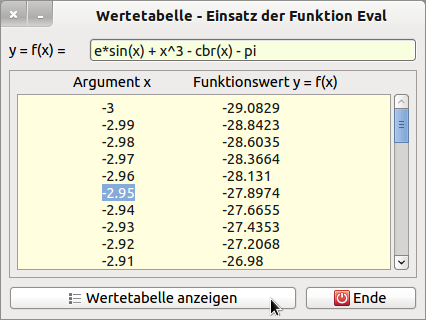
Abbildung 19.8.1.2: Wertetabelle – Funktion Eval(..)

Sehen Sie – es funktioniert! Doch folgende Erweiterungen sind m.E. für den Einsatz im Projekt „Funktionsplotter“ vorzunehmen:

• Festlegung des Zeichenbereiches (anfangX, endeX),
• Festlegung der Schrittweite deltaX,
• Überlaufgrenzen für die Funktionswerte festlegen,
• Wertepaare in einem Array speichern,
• Option: Statt einer TextArea eine GridView einsetzen, wenn Wertetabelle angezeigt werden soll,
• Es fehlt noch eine Fehlerbehandlung, wenn sich zum Beispiel kein f(x) berechnen lässt und diese nicht validen Funktionswerte kennzeichnen sowie speichern,
• Option2: Die Berechnung und Speicherung der Wertepaare in ein Modul oder in eine eigene Klasse auslagern, um Modul oder Klasse dann auch in anderen Projekten zu verwenden.
• Alternative: Einsatz der Klasse Expression (gb.eval) für die Funktion Eval(..)

Die o.a. Erweiterungen sind in einem Projekt „Funktionsplotter“ umgesetzt worden, das mehrere eigene Klassen nutzt und im Kapitel 26 beschrieben ist.