GAMBAS-BUCH 3.19.1

Wenn Sie Ihrem rastlosen informatischen Tun eine klare Richtung und ein Ziel geben wollen, dann sollten Sie sich Algorithmen mit einem rekursiven Ansatz zuwenden, um Ihr Gehirn in alle Richtungen heftig zu verbiegen. Die Rekursion ist ein allgemeines Verfahren, um eine Aufgabe schrittweise in elementar lösbare Teilaufgaben zu zerlegen und auf jede Teilaufgabe den gleichen Algorithmus anzuwenden. In der Informatik ist die Rekursion eine Alternative zur Kontrollstruktur Wiederholung oder Iteration. Die Algorithmen mit rekursivem Ansatz sind zwar eleganter in der Formulierung und oft kürzer, aber schwerer inhaltlich zu verstehen. Das wird auch an den zwei vorgestellten Beispielen aus der Mathematik deutlich, bei denen zuerst die mathematische Aufgabe beschrieben wird, dann eine induktiv formulierte Funktion abgeleitet wird und abschließend der Algorithmus zur Berechnung der Funktionswerte vorgestellt wird.

Die Berechnung der Summe natürlicher Zahlen von 1 bis i lässt sich als Funktion summe(i) = 1+2+…+i induktiv so definieren:

• summe(0) = 0
• summe(i) = i + summe(i - 1) für i > 0

Berechnung der Funktionswerte von summe(i):

PUBLIC FUNCTION summe(i AS Integer) AS Integer 
  IF i = 0 THEN 
     RETURN 0 
  ELSE 
    RETURN i + summe(k - 1) ' Rekursiver Aufruf mit reduziertem Argument! 
  ENDIF 
END ' summe(..) 

Die Berechnung des Produktes der natürlichen Zahlen von 1 bis k als produkt(k) = 1 * 2 * 3 * … * k nennt k-Fakultät und beschreibt es mit dem Symbol k! . Die Funktion fakultät(k) kann so induktiv definiert werden:

• fakultät(0) = 1 und fakultät(1) = 1
• fakultät(k) = k * fakultät(k-1) für k > 1

Berechnung der Funktionswerte von fakultät(k):

PUBLIC FUNCTION fakultaet(k AS Integer) AS Integer 
  IF k = 0 OR k = 1 THEN 
     RETURN 1 
  ELSE 
    RETURN k * fakultaet(k - 1) ' Rekursiver Aufruf mit reduziertem Argument! 
  ENDIF 
END ' fakultaet(..) 

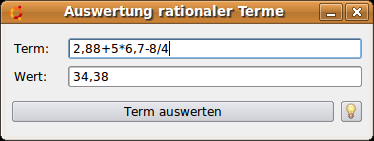
Die Aufgabe ist recht einfach: Berechnung des Wertes eines Ausdrucks mit folgendem Eingabe-Alphabet = {0..9, + , - , * , / , Komma} unter der Beachtung der Wertigkeit oder Rangfolge der Operationen. Die Lösung basiert auf der Methode des rekursiven Abstiegs und liefert zum Beispiel für den Ausdruck 2,88+5*6,7-8/4 als Wert die rationale Zahl 34,38:

Abbildung 10.4.3.1: Auswertung für einen Ausdruck

Es wird im folgenden Abschnitt der vollständige Quelltext angegeben. Bitte beachten Sie, dass keine Überprüfung der Eingabezeichen des eingegeben Ausdrucks erfolgt und auch keine Fehlerbehandlung eingebaut ist, um den Quelltext so einfach wie möglich und gut lesbar zu halten.

Quelltext:

' Gambas class file 
 
PUBLIC SUB Form_Open() 
  FMain.Center 
  FMain.Border = 1 
  txtTerm.SetFocus 
END 
 
PUBLIC SUB btnInfoAnzeigen_Click() 
  Balloon.Info("Eingabe-Alphabet:" & Chr(10) & "0..9, + , - , * , / , Komma", LAST) 
END 
 
PUBLIC SUB txtTerm_Change() 
  txtWert.Clear 
END 
 
PUBLIC FUNCTION anfang(zeichenkette AS String, zeichen AS String) AS String 
  DIM position, anzahl AS Integer  
  position = InStr(zeichenkette, zeichen) 
  anzahl = position - 1 
  RETURN Mid$(zeichenkette, 1, anzahl)  
END 
 
PUBLIC FUNCTION copyab(zeichenkette AS String, i AS Integer) AS String 
  DIM anzahl AS Integer 
  anzahl = Len(zeichenkette) - i + 1 
  RETURN Mid$(zeichenkette, i, anzahl) 
END 
 
PUBLIC FUNCTION ende(zeichenkette AS String, zeichen AS String) AS String 
  DIM position, anzahl AS Integer 
  position = InStr(zeichenkette, zeichen) 
  anzahl = position + 1 
  RETURN copyab(zeichenkette, anzahl) 
END 
 
PUBLIC FUNCTION TermToReell(s AS String) AS Float 
  IF InStr(s, "+") > 0 THEN 
     RETURN TermToReell(anfang(s, "+")) + TermToReell(ende(s, "+")) 
  ELSE IF InStr(s, "-") > 0 THEN 
    RETURN TermToReell(anfang(s, "-")) - TermToReell(ende(s, "-")) 
  ELSE IF InStr(s, "/") > 0 THEN 
    RETURN TermToReell(anfang(s, "/")) / TermToReell(ende(s, "/"))
  ELSE IF InStr(s, "*") > 0 THEN 
    RETURN TermToReell(anfang(s, "*")) * TermToReell(ende(s, "*")) 
  ELSE 
    RETURN Val(s) 
  ENDIF 
END 
 
PUBLIC SUB btnTermAuswerten_Click() 
  txtWert.Text = Str(TermToReell(txtTerm.Text))  
END 

Die Hauptlast der Berechnung des Wertes des eingegebenen Ausdrucks trägt die Funktion TermToReell(ausdruck), die mit ständig wechselnden Argumenten rekursiv aufgerufen wird. Erkunden Sie für den einfachen Ausdruck 1+2*3-4/5, wie der Wert 6,2 berechnet worden ist. Dazu ist es notwendig, sich auch mit den verwendeten 3 Funktionen zur Bearbeitung von Zeichenketten zu befassen, um zu ergründen was diese Funktionen leisten.

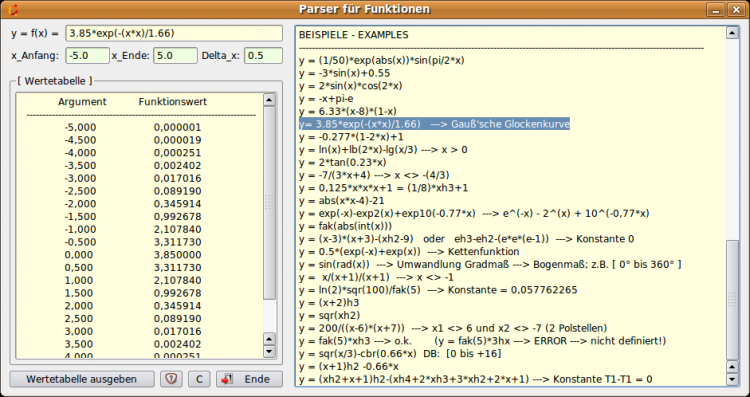
Die vorgestellten Algorithmen gehören zu einem Teilprojekt für einen Funktionsparser, mit dem Funktionswerte für eine vorgegebene Funktion f berechnet werden konnten. Das vollständige Projekt finden Sie im Download-Bereich zusammen mit den Projekten Term0 – aus dem der o.a. Quelltext stammt – und Term0E. Das Projekt Term0E enthält einen Zeichen-Scanner und notwendige Fehlerbehandlungsprozeduren.

Als Vorteil des entwickelten und getesteten Funktionsparsers kann die Definition von speziellen Funktionen wie fakultät(k) genannt werden, die zum Beispiel in der Komponente gb.eval nicht vorhanden sind.

Abbildung 10.4.3.2: Berechnung einer Wertetabelle mit angezeigter Hilfe (ausklappbar)