This chapter presents three projects that demonstrate the use of options and arguments for Gambas programs in different ways.

Another interesting variant is presented in the' Chapter 2.6 Sharing Gambas programs - installation package' in a well-documented project.

In this project for color selection in a ColorChooser, you can optionally transfer exactly 3 color values (RGB) to the program in order to define an individual start value for the color to be displayed after the program start.

• If an argument is missing or if two or all 3 arguments are missing, a valid start color value is defined.
• With the values of the 3 arguments - if no error occurred - a color value is calculated, which serves as default color for the used component ColorChooser1.
• In this project, the three arguments are not checked to see whether they only accept valid RGB values[0… 255].

The source code of the Gambas project' ColorSelectA1' is similar to the script in chapter 5.8.0.

' Gambas class file
 
Public Sub Form_Open()
  Dim sArgument As String
  Dim R, G, B As Integer
 
  FMain.Center
  FMain.Resizable = False
 
  FMain.Text = "Programme with 3 arguments (optional)"
 
  If Application.Args.Count <> 4 Then
     Print "Error! At least 1 argument is missing."
     R = 220
     G = 20
     B = 180
  Else
     R = Val(Application.Args[1])
     G = Val(Application.Args[2])
     B = Val(Application.Args[3])
  Endif ' Application.Args.Count <> 4 ?
 
  ColorChooser1.SelectedColor = Color.RGB(R, G, B)
 
End ' Form_Open

With Application. Args, Gambas provides an object with all the arguments of the Gambas program that you can use like an array:

• The first argument Application. Args[0] is (= $0) is always the name of the started Gambas program.
• The property Application. Args. Count returns the number of all arguments - not only those passed directly in the console! For this reason, the above-mentioned source code is also checked with Application.

In this point, working with the array of arguments in Gambas differs from determining the number of arguments for a bash script in the console!

When called in a console:

hans@linux:~$ gbx3 $HOME/ColorSelectA1 -- 225 110 60

the Gambas interpreter starts the program for color selection with the default color ochre:

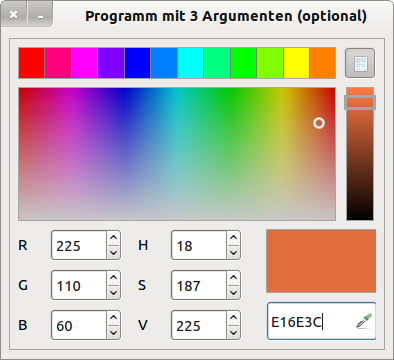
Figure 5.8.2.1.1: Color selection program - default color via 3 arguments

The next time you call up the program, you receive a note and the program is started with a standard color value (? source code) in this case:

hans@linux:~$ gbx3 $HOME/E/ColorSelectA1 -- 50 120
Hint! At least 1 argument is missing.

The special features of this second project can be described in this way:

• 2 properties of the class Args of the component gb are used.
• The arguments passed to the program are checked according to different criteria.
• If an error occurs, then this error is only displayed with a hint and a permissible start color value is set in order to create clearly defined conditions for the program start.
• Due to the error vector used, it is possible to perform a differentiated error analysis.

The source code reflects the above-mentioned special features:

' Gambas class file
 
Public aArgumente As String[]
 
Public Sub Form_Open()
  FColor.Center
  FColor.Resizable = False
  FColor.Text = "Programme with 3 arguments (optional)"
 
' String array as a copy of the array of all arguments
  aArgumente = Args.All ' aArgumente[0] = ProgrammName
 
  If GetErrorVector(aArgumente).ToString(True) = "[0 0 0 0 0 0 0]" Then
     ColorChooser1.Value = Color.RGB(Val(aArgumente[1]), Val(aArgumente[2]), Val(aArgumente[3]))
  Else
     ErrorAnalysis(GetErrorVector(aArgumente))
  Endif ' Without error ?
 
End ' Form_Open
 
Public Sub ColorChooser1_Change()
  Dim cColor As Integer
 
  cColor = ColorChooser1.SelectedColor ' Synonym for ColorChooser1.Value, DataType: Integer
 
End ' ColorChooser1_Change()
 
Private Function GetErrorVector(aArgs As String[]) As Vector
  Dim vFA As Vector ' vFA → Error-Array
  Dim i As Integer = 1
 
  vFA = New Vector(7, False)
  vFA = [0, 0, 0, 0, 0, 0, 0]
' (1) Determine number of arguments
  If aArgs.Count = 1 Then vFA = [3, 0, 0, 0, 0, 0, 0]
  If aArgs.Count = 2 Then vFA = [2, 0, 0, 0, 0, 0, 0]
  If aArgs.Count = 3 Then vFA = [1, 0, 0, 0, 0, 0, 0]
 
  If aArgs.Count = 4 Then
     For i = 1 To aArgs.Max
       If Not IsInteger(aArgs[i]) Then ' (2) Check whether integer number
          vFA[i] = 1
       Else
          If Val(aArgs[i]) < 0 Or Val(aArgs[i]) > 255 Then ' (3) Test for the interval [0..255]
             vFA[i + 3] = 1
          Endif
       Endif
     Next
  Endif
 
  Return vFA ' Return Error Vector
 
End ' Function Error Vector(..)
 
Private Sub ErrorAnalysis(vVektor As Vector)
  Dim i, j As Integer
 
  Print "ERROR!"
' Differentiated evaluation error vector: element A0 (number of missing arguments)
  If vVektor[0] <> 0 Then
     If vVektor[0] = 1 Then
        Print "It lacks precisely "; vVektor[0]; " Argument!"
        Inc j
     Else
       Print "It lacks precisely "; vVektor[0]; " Arguments!"
       Inc j
     Endif
  Endif
' Evaluation Error Vector: A1-A3 (Which argument cannot be converted to integer?)
  For i = 1 To 3
    If vVektor[i] <> 0 Then
       Print "Das "; i; ". Argument is not an integer."
       Inc j
    Endif
  Next
' Evaluation error vector: A4-A6 (Which argument is not in the interval [0..255]?)
  For i = 4 To 6
    If vVektor[i] <> 0 Then
       Print "Das "; i - 3; ". Argument is not in the interval [0..255]!"
       Inc j
    Endif
  Next
 
  Print "Therefore, 3 standard colour values are used."
  ColorChooser1.Value = Color.RGB(220, 20, 180) ' Start arguments - colour: pink
 
End ' ErrorAnalysis(vVektor As Vector)

Here you can see three calls of the program for color selection in the console and the corresponding program reactions depending on the number and type of arguments passed:

hans@linux:~$ gbx3 $HOME/E/ColorSelectA2 -- 222 133
Hint!
Exactly 1 argument is missing!
Therefore 3 default colour values are used.
hans@linux:~$

hans@linux:~$ gbx3 $HOME/E/ColorSelectA2 -- 22O, 344 1E2
Hint!
The 1st argument is not an integer.
The 3rd argument is not an integer number.
The 2nd argument is not in the interval [0..255]!
Therefore 3 standard colour values are used.
hans@linux:~$

hans@linux:~$ gbx3 $HOME/E/ColorSelectA2 -- "50 120 30" ' Exactly 1 character string is transferred
Hint!
Exactly 2 arguments are missing!
Therefore 3 standard colour values are used.
hans@linux:~$

At these two program starts, the arguments determine the same default color:

hans@linux:~$ gbx3 $HOME/E/ColorSelectA2 -- "50" "120" "30"
hans@linux:~$ gbx3 $HOME/E/ColorSelectA2 -- 50 120 30

Project 3 (? Chapter 24.8.1 Projects to demonstrate the component gb. map) allows you to display maps of openstreetmap. org (OSM). To view a map you need

• the value for the latitude of the starting point,
• the value for the longitude of the starting point,
• the zoom value from the interval[1.. 18] and
• an active Internet connection to retrieve the (pre-)calculated cards from the OSM server.

It makes sense, depending on the intended purpose

• you can use an option to specify whether the geographical starting point (or another special point) on the map is marked with a symbol, and
• to interactively pass the coordinates for the geographical starting point on the map and the zoom factor to the Gambas program as an argument:

hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52,7904 11,7533 15
hans@linux:~$ gbx3 $HOME/E/OSMapA -- -s n -- 52.7904 11.7533 15

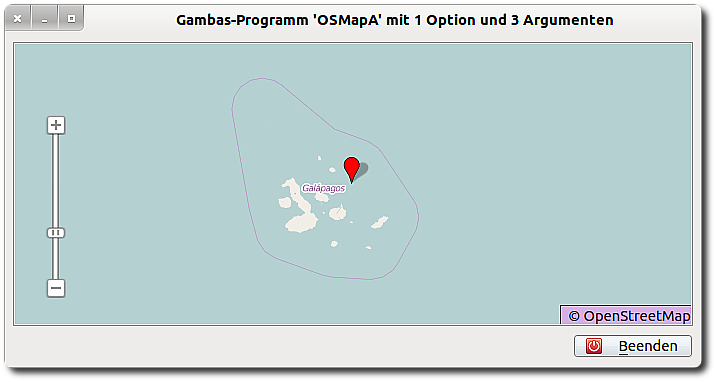
Figure 5.8.2.3.3.1: Galapagos (– –shape j – 0.01 -90.002 7)

The project archive can be found in the download area. If you unpack the archive into the $HOME/E path, you can immediately test the program with these calls in a console:

hans@linux:~$ gbx3 $HOME/E/OSMapA
hans@linux:~$ gbx3 $HOME/E/OSMapA -- -h
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --help
hans@linux:~$ gbx3 $HOME/E/OSMapA -- -v
hans@linux:~$ gbx3 $HOME/E/OSMapA -- -V
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --version

hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52,7904 1,0 6
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape n -- 52.7904 1.0 6
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 0 0 3

hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- -30,0 -50,9 3
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape y -- 52.7904 1.0 6

hans@linux:~$ gbx3 $HOME/E/OSMapA -- -- 52.7904 1.0 6
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape n
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape -- 52.7904 1.0 6

hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 0.01 -90.002 7

hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52.7904 331.0 6
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52.7904 12

hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52.7904 1.0 1o
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52.7904 1.0 19
hans@linux:~$ gbx3 $HOME/E/OSMapA -- --shape j -- 52.7904 1.0 11.5

hans@linux:~$ gbx3 $HOME/E/OSMapA -- -30,0 -50,9 4
hans@linux:~$ gbx3 $HOME/E/OSMapA -- 30,0 50,9 4

In the project source code, you can see that the error functions in error handling provide numeric values as function values, as shown in the following section of the source code:

Private Function IsDecimalDegree(sDegree As String, sFlag As String) As Integer
  If Upper(sFlag) Not Like "{LAT,LON}" Then Return 1

  If Upper(sFlag) = "LAT" Then
     If IsFloat(sDegree) Then
        If (Val(sDegree) <= -90) Or (Val(sDegree) > 90) Then
           Return 2
        Else
           Return 0
        Endif
     Else
        Return 3
     Endif
  Endif

  If Upper(sFlag) = "LON" Then
     If IsFloat(sDegree) Then
        If (Val(sDegree) <= -180) Or (Val(sDegree) > 180) Then
           Return 4
        Else
           Return 0
        Endif
     Else
        Return 5
     Endif
  Endif

End ' Function IsDecimalDegree(..)