In a “function plotter” project, problems arose at a point that had not been in view before. While the plotter of a function y = f(x), which is hard-coded in the source code

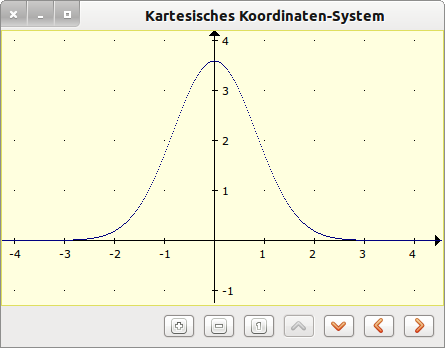
Public Function f(x As Float) As Float ' Das Argument ist x
  RETURN (9 / Sqr(2 * pi)) * Exp(- (x * x) / 1.66)
End

with zoom and shift worked well, the interactive input of the function to be drawn and the calculation of the function values proved to be a problem in order to be able to use the function plotter universally!

Figure 19.8.1.1: Density function (normal distribution)

First promising approaches emerged in connection with the direct evaluation of (Gambas) expressions. Hints and examples for the evaluation of (Gambas) expressions can be found in chapter 25.5.3.

The Gambas help for the interpreter states:

If you call the Gambas interpreter gbx3 in a terminal with the option -e, then you can evaluate an <expression> passed as a parameter and display the result:

  Verwendung:	gbx3 -e <Ausdruck>
  Option: 	-e   einen Ausdruck auswerten

Here follows a tried and tested example:

hans@linux:~$ gbx3 -e "2.44-sin(pi/3)"
1,57397459621556

Here the -e option stands for the use of the function Eval(..) . When you call this function, the gb.eval component is automatically loaded:

Value = Eval ( Expression AS String [ , Context AS Collection ] ) AS Variant

The text in the Gambas help supports this view:

Eval(..) evaluates an expression and returns its value. This expression can contain almost all of Gambas' operators and subroutines. The optional context is a collection that must contain the value of each of the undefined symbols.

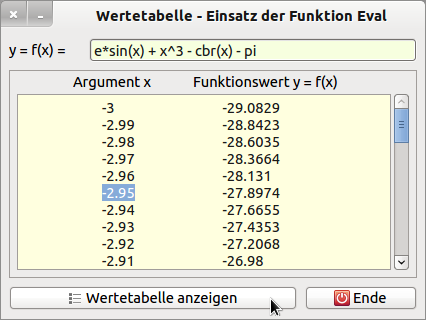
However, the most interesting part is the last sentence! If you look closely at the assignment rule in another function y = g(x) = e*sin(x) + x^3 - cbr(x) - pi, the algebraic expression also contains the functions sin(x), power function x^3 and the root function cbr(x) with the root exponent (1/3) known in Gambas. The symbol pi is also known! The parameter e as Euler's number and the variable x are obviously the symbols not defined above. These have to be defined p.d. via the context. This results in the following first solution approach for the calculation of the value table for the function g(x). With its value pairs, the image of the function can later be drawn iteratively in the project “Function Plotter”.

The following source code belongs to a test project that proved to realise an interactive input of a function and to use the function Evel() successfully to calculate function values. Here is the complete and sufficiently commented source code:

' Gambas class file
 
Public Sub Form_Open()
  FMain.Center
  FMain.Resizable = False
  txbFunction.Text = "e*Sin(x) + x^3 - Cbr(x) - Pi" ' Default-Function
End
 
Public Sub btnComputeTOV_Click() ' TOV → TableOfValues
  Dim y As Float
  Dim Context As New Collection
 
  txaTableOfValues.Clear
  Context["e"] = Exp(1) ' Dem Symbol e wird der Wert e=Exp(1) (= e^1)zugewiesen
  Context["x"] = -3     ' Dem Symbol x wird der Wert -3 zugewiesen
 
  Repeat
    Try y = Eval(txbFunction.Text, Context) ' Interaktive Eingabe von f(x) in txbFunction.Text
    If Error Then
       Message.Error("Das ging in die Hose...!")
       Return
    Endif ' ERROR
    txaTableOfValues.Insert(gb.Tab & Round(CFloat(Context["x"]), -3) & gb.Tab & "         " \
                            & Round(CFloat(y), -4) & gb.NewLine)
    Context["x"] = Context["x"] + 0.01 ' Dem Symbol x wird ein erhöhter Wert zugewiesen
  Until Context["x"] > 3.001 ' Abbruch, wenn das Symbol x einen Wert > 3.001 hat
 
End
 
Public Sub txbFunction_Change()
  txaTableOfValues.Clear
End
 
Public Sub btnClose_Click()
  FMain.Close
End

Figure 19.8.1.2: Value table - function Eval(..)

You see - it works! But I think the following extensions have to be made for use in the “function plotter” project:

• Definition of the drawing area (beginX, endX),
• definition of the step size deltaX,
• set overflow limits for the function values,
• store pairs of values in an array,
• Option: Use a GridView instead of a TextArea if a table of values is to be displayed,
• Error handling is still missing if, for example, no f(x) can be calculated and mark as well as save these non-valid function values,
• Option2: Outsource the calculation and storage of the value pairs to a module or to a separate class, so that the module or class can then also be used in other projects.
• Alternative: Use the Expression class (gb.eval) for the Eval(..) function.

The above extensions have been implemented in a project called “Funktionsplotter”, which uses several of its own classes and is described in chapter 26.