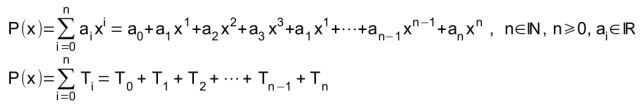Inhaltsverzeichnis
29.3.4 Polynomial
Die Klasse Polynomial aus gb.gsl implementiert ein Polynom mit reellen oder komplexen Koeffizienten. Sie agiert wie ein Lese-/Schreib-Array und kann wie eine Funktion verwendet werden. Die Klasse Polynomial verfügt über zwei Eigenschaften und drei Methoden.
29.3.4.1 Polynom
Ein Polynom oder besser eine Polynom-Funktion P(x) kann so definiert werden:
- Die reellen oder komplexen Zahlen ai nennt man Koeffizienten.
- Die natürlichen Zahlen n, n-1, n-2, …,1 und 0 sind mögliche Exponenten.
- Der größte Wert der Exponenten bestimmt den Grad des Polynoms.
- Die Ti bezeichnet man als Term oder Monom mit Tk = akxk .
- Polynom und Polynom-Funktion P(x) werden synonym verwendet.
29.3.4.2 Eigenschaften
Die Klasse Polynomial verfügt über zwei Eigenschaften:
| Eigenschaft | Datentyp | Beschreibung |
|---|---|---|
| Count | Integer | Gibt die Anzahl der Koeffizienten zurück. |
| Degree | Integer | Gibt den Grad des Polynoms als Wert (n ≥ 0 , n Î N) des größten Exponenten zurück. |
Tabelle 29.3.4.2.1 : Eigenschaften der Klasse Polynomial
29.3.4.3 Methoden
Die Klasse Polynomial verfügt über diese drei Methoden:
| Methode | Rückgabetyp | Beschreibung |
|---|---|---|
| Eval ( x As Variant ) | Variant | Berechnet den Wert eines Polynoms P(x) für das gegebene Argument x. |
| Solve ( [ Complex As Boolean ] ) | Array | Es werden die reellen Wurzeln des Polynoms mit P(x)=0 berechnet und zurückgegeben. |
| ToString ( [ Local As Boolean ] ) | String | Zurückgegeben wird das Polynom als String-Repräsentation. |
Tabelle 29.3.4.3.1 : Methoden der Klasse Polynomial
Hinweise:
- Der Rückgabetyp der Methode Eval (..) ist vom Typ Variant, weil der Wert einer Polynom-Funktion P(x) eine reelle oder eine komplexe Zahl sein kann.
- Werden keine Wurzeln gefunden, dann wird ein leeres Array zurückgegeben.
Wenn P(x) = 0 die folgenden Strukturen aufweist, werden die Wurzeln exakt berechnet:
x³ + a*x² + b*x + c = 0 oder a*x² + b*x + c = 0
- In allen anderen Fällen werden Näherungsverfahren eingesetzt, die nicht notwendigerweise für den (intern) gesetzten Startwert konvergieren! In diesen (divergenten) Fällen wird ein Fehler ausgelöst. Das Auftreten mehrerer gleicher Wurzeln wird nicht als etwas Besonderes herausgestellt wie zum Beispiel bei der Gleichung (x-1)³ = 0, die genau drei gleiche reelle Wurzeln als Lösungen besitzt.
- Alle Wurzel-Werte als Lösungen von P(x)=0 sind abschließend unbedingt zu prüfen (Probe).
- Oft wird bei den Lösungen nur eine hinreichend genaue Lösung – zum Beispiel bei der Gleichung x³-x=0 mit x2= -7.0705015914994E-17 – ausgegeben, während die beiden anderen Lösungen mit x1=-1 und x3=+1 exakte Wurzel-Werte liefern.
- Hat der Parameter Local den Wert True, dann werden die Zahlen in der lokalen Notation ausgegeben, während der Standard-Wert False den String so formatiert, dass er von der Funktion Eval(..) ausgewertet werden kann.
29.3.4.4 Erzeugen von Polynomen
Es gibt mehrere Möglichkeiten Polynome zu erzeugen:
- Deklaration einer Variablen vom Daten-Typ Polynomial mit direkter Wertzuweisung.
- Deklaration einer Variablen vom Daten-Typ Polynomial und spätere Zuweisung der Koeffizienten in einem Array (mit steigenden Potenzen und Komma als Separator), wobei fehlende Terme durch 0 repräsentiert werden müssen! Der Grad des Term ergibt sich aus seiner Stelle im Array.
- Konvertierung einer Zeichenkette aus einer geeigneten (Eingabe-)Komponente in ein Polynom.
Beispiel für die Umsetzung der ersten beiden Möglichkeiten unter Einbeziehung der beiden Eigenschaften Count und Degree sowie der Methode ToString(..):
Dim pPolynom1 As Polynomial = [-8.88, 1, 0, 0, 0.44, -6.66] ' Möglichkeit 1 Dim pPolynom2 As Polynomial ' Möglichkeit 2.1 Dim aRoots As Complex[] Dim iCount As Integer Print "Polynom 1 = ";; pPolynom1 Print "Polynom 1 = ";; pPolynom1.ToString(True) Print "Polynom 1 = ";; pPolynom1.ToString() ' False ist Standard-Parameter, Angabe optional Print pPolynom1.Degree ' Grad des Polynoms Print pPolynom1.Count ' Anzahl der Terme des Polynoms pPolynom2 = [-9, -9, 1, 1] ' Möglichkeit 2.2 Print "Polynom 2 = ";; pPolynom2 Print "Polynom 2 = ";; pPolynom2.ToString(True) Print "Polynom 2 = ";; pPolynom2.ToString()
Das sind die Ausgaben in der Konsole der Gambas-IDE:
[1] Polynom 1 = -6,66x^5+0,44x^4+x-8,88 [2] Polynom 1 = -6,66x^5+0,44x^4+x-8,88 [3] Polynom 1 = -6.66*x^5+0.44*x^4+x-8.88 [4] 5 [5] 6 [6] Polynom 2 = x^3+x^2-9x-9 [7] Polynom 2 = x^3+x^2-9x-9 [8] Polynom 2 = x^3+x^2-9*x-9
29.3.4.5 Berechnung des Funktionswertes einer Polynom-Funktion P(x)
Die Berechnung des Funktionswertes einer Polymom-Funktion P(x) wird für reelle und für komplexe Argumente gezeigt:
Dim pPolynom2, pPolynom3 As Polynomial pPolynom2 = [-9, -9, 1, 1] Print "Polynom 2 = ";; pPolynom2.ToString(True) Print "P2(2,34) = "; Eval(pPolynom2.ToString(False), ["x": 2.34]) ' Reelles Argument Print pPolynom3 = [-9i, 2, 1 - 2i] Print "Polynom 3 = ";; pPolynom3.ToString(False) Print "P3(1+i) = "; Eval(pPolynom3.ToString(False), ["x": 1 + 1i]) ' Komplexes Argument
Hier die Ausgaben:
[1] Polynom 2 = x^3+x^2-9x-9 [2] P2(2,34) = -11,771496 [3] [4] Polynom 3 = (1-2i)*x^2+2*x-9i [5] P3(1+i) = 6-5i
29.3.4.6 Berechnung der Nullstellen einer Polynom-Funktion
Die Berechnung der Nullstellen einer Polynom-Funktion oder die Berechnung der Lösungen einer Polynom-Gleichung führt auf P(x)=0.
- Der Erfolg der Methode Solve(..) ist an diese Voraussetzung gebunden: Alle Koeffizienten in der Polynom-Funktion P(x) sind reelle Zahlen, sonst wird ein Fehler ausgelöst!
- Ist der Parameter Complex True, dann werden alle komplexen Wurzeln berechnet und in einem Array zurückgegeben. Ist der Parameter Complex False, dann werden nur die existierenden reellen Wurzeln berechnet und in einem Array zurückgegeben.
Die Berechnung der Lösungen von P(x)=0 wird für reelle und für komplexe Argumente gezeigt:
Dim pPolynom2, pPolynom4 As Polynomial Dim aRoots As Complex[] Dim iCount As Integer pPolynom2 = [-9, -9, 1, 1] Print "Polynom 2 = ";; pPolynom2.ToString(True) aRoots = pPolynom2.Solve(False) ' Nur reelle Wurzeln For iCount = 0 To aRoots.Max Print "Wurzel_" & CInt(iCount + 1) & " = " & aRoots[iCount] Next ' iCount Print pPolynom4 = [4, 0, 1] Print "Polynom 4 = ";; pPolynom4.ToString(True) aRoots = pPolynom4.Solve(True) ' Nur komplexe Wurzeln For iCount = 0 To aRoots.Max Print "Wurzel_" & CInt(iCount + 1) & " = " & aRoots[iCount] Next ' iCount
In der Konsole lesen Sie dann:
Polynom 2 = x^3+x^2-9x-9 Wurzel_1 = -3 Wurzel_2 = -1 Wurzel_3 = 3 Polynom 4 = x^2+4 Wurzel_1 = -2i Wurzel_2 = 2i
Setzen Sie für aRoots = pPolynom4.Solve(True) dagegen aRoots = pPolynom4.Solve(False), dann erhalten Sie als Lösungsmenge die leere Menge – respektive in Gambas ein leeres Array – weil für die Potenz-Funktion P(x)=x⁴+4=0 keine reellen Lösungen existieren.
29.3.4.7 Beispiel
Das folgende Beispiel setzt die dritte Variante zur Erzeugung eines Polynoms über die Konvertierung einer Zeichenkette aus einer geeigneten (Eingabe-)Komponente – hier EingabeBox – in ein Polynom um. Kernstück der 3. Variante sind die folgenden zwei Funktionen, in denen einerseits geprüft wird, ob eine Zeichenkette als Polynom interpretiert werden kann und andererseits die Koeffizienten einer Polynom-Funktion P(x) bestimmt werden – sofern sich die eingegebene Zeichenkette als Polynom interpretieren lässt – wobei nur reelle Koeffizienten zugelassen sind:
Private Function ValPolynomial(sInput As String) As Polynomial ' Tobias Boege Private Function IsPolynomial(sInput As String) As Boolean
Hier der vollständige, hinreichend kommentierte Quelltext:
' Gambas class file Private $pP1 As Polynomial Private $pP2 As Polynomial Private $pResult As Polynomial Public Sub Form_Open() FMain.Center FMain.Resizable = False ' txbInputPolynom1.Clear ' Freischalten... ' txbInputPolynom2.Clear ' Freischalten... txbInputPolynom1.SetFocus ' http://de.wikipedia.org/wiki/Unicodeblock_Mathematische_Operatoren btnAddieren.Text = " Polynome addieren " & String.Chr(8853) btnSubtrahieren.Text = " Polynome subtrahieren " & String.Chr(8854) End ' Form_Open() Public Sub btnConvert_Click() If txbInputPolynom1.Text Then txbOutputPolynom.Clear Try txbOutputPolynom.Text = ValPolynomial(txbInputPolynom1.Text).ToString() If Error Then Message.Error("Der String für P1(x) kann\nnicht\nals Polynom interpretiert werden!") txbInputPolynom1.SetFocus Endif ' ERROR ? Endif ' Text ? End ' btnConvert_Click() Public Sub txbInputPolynom1_Activate() btnConvert_Click() End ' txbInputPolynom1_Activate() Public Sub txbInputPolynom1_KeyPress() CheckInput("+-,.^0123456789x") End ' txbInputPolynom1_KeyPress() Public Sub txbInputPolynom2_KeyPress() CheckInput("+-,.^0123456789x") End ' txbInputPolynom2_KeyPress() Public Sub btnIsPolynomial_Click() If txbInputPolynom1.Text Then If IsPolynomial(txbInputPolynom1.Text) = True Then Message.Info("Der Eingabe-String für P1(x) kann als\nPolynom\ninterpretiert werden!") Else Message.Error("Der String für P1(x) kann\nnicht\nals Polynom interpretiert werden!") txbInputPolynom1.SetFocus Endif ' IsPolynomial(txbInputPolynom1.Text) ? Endif ' txbInputPolynom1.Text ? End ' btnIsPolynomial_Click() Public Sub btnAddieren_Click() If txbInputPolynom1.Text And txbInputPolynom2.Text Then If (IsPolynomial(txbInputPolynom1.Text) = True) And (IsPolynomial(txbInputPolynom2.Text) = True) Then $pP1 = ValPolynomial(txbInputPolynom1.Text) $pP2 = ValPolynomial(txbInputPolynom2.Text) $pResult = $pP1 + $pP2 txbOutputPolynom.Text = $pResult.ToString() Else Message.Error("Mindestens ein Eingabe-String kann\nnicht\nals Polynom interpretiert werden!") Endif ' IsPolynomial(..) ? Endif ' Text ? End ' btnAddieren_Click() Public Sub btnSubtrahieren_Click() If txbInputPolynom1.Text And txbInputPolynom2.Text Then If (IsPolynomial(txbInputPolynom1.Text) = True) And (IsPolynomial(txbInputPolynom2.Text) = True) Then $pP1 = ValPolynomial(txbInputPolynom1.Text) $pP2 = ValPolynomial(txbInputPolynom2.Text) $pResult = $pP1 - $pP2 txbOutputPolynom.Text = $pResult.ToString() Else Message.Error("Mindestens ein Eingabe-String kann\nnicht\nals Polynom interpretiert werden!") Endif ' IsPolynomial(..) ? Endif ' Text ? End ' btnSubtrahieren_Click() Public Sub btnVergleichen_Click() If txbInputPolynom1.Text And txbInputPolynom2.Text Then If (IsPolynomial(txbInputPolynom1.Text) = True) And (IsPolynomial(txbInputPolynom2.Text) = True) Then If ValPolynomial(txbInputPolynom1.Text) = ValPolynomial(txbInputPolynom2.Text) Then txbOutputPolynom.Text = "P1(x) und P2(x) sind gleich!" Else txbOutputPolynom.Text = "P1(x) und P2(x) sind NICHT gleich!" Endif Else Message.Error("Mindestens ein Eingabe-String kann\nnicht\nals Polynom interpretiert werden!") Endif ' IsPolynomial(..) ? Endif ' Text ? End ' btnVergleichen_Click() '********************************************************************************************************* Public Sub txbInputPolynom1_Change() txbOutputPolynom.Clear End ' txbInputPolynom1_Change() Public Sub txbInputPolynom2_Change() txbOutputPolynom.Clear End ' txbInputPolynom2_Change() Public Sub CheckInput(sAllowed As String) ' Idee Charles Guerin Select Case Key.Code Case Key.Left, Key.Right, Key.BackSpace, Key.Delete, Key.End, Key.Home, Key.Enter, Key.Return Return Default If Key.Text And If InStr(sAllowed, Key.Text) Then Return Endif End Select Stop Event End ' CheckInput(sAllowed As String) Private Function ValPolynomial(sInput As String) As Polynomial Dim hRegexp As New RegExp Dim hPolynom As New Polynomial(1) Dim fKoeffizient As Float Dim iExponent As Integer Dim sMiddle As String ' Dezimalseparator der aktuellen Locale durch den Punkt ersetzen sInput = Replace$(sInput, Left$(Format$(0, ".0")), ".") ' Eingabe normieren: Der erste Term (Monom) im Polynom benötigt ein Vorzeichen If Left$(sInput) Not Like "[+-]" Then sInput = "+" & sInput hRegexp.Compile("([+-][0-9]+(\\.[0-9]+)?)(x)?(\\^([0-9]+))?|[+-]x(\\^([0-9]+))?") hRegexp.Exec(sInput) While hRegexp.Offset <> -1 ' Wenn kein Koeffizient im Term eingegeben ist, dann Koeffizient = 1, ' Wenn kein Exponent im Term eingegeben ist, dann Exponent = 1, ' Wenn das Argument x nicht im Term enthalten ist, dann Exponent = 0. If hRegexp[0].Text Like "[+-]x*" Then fKoeffizient = IIf(hRegexp.Text Begins "+", 1.0, -1.0) If hRegexp.Count = 7 Then iExponent = CInt(Right$(hRegexp[6].Text, -1)) Else iExponent = 1 Endif Else fKoeffizient = CFloat(hRegexp[1].Text) If hRegexp.Count = 5 Then iExponent = CInt(Right$(hRegexp[4].Text, -1)) Else If hRegexp.Count = 3 Then iExponent = 1 Else iExponent = 0 Endif Endif hPolynom[iExponent] += fKoeffizient sMiddle = Mid$(sInput, hRegexp.Offset sInput = Mid$(sInput, 1, hRegexp.Offset) & sMiddle + Len(hRegexp[0].Text) + 1) If Not sInput Then Return hPolynom hRegexp.Exec(sInput) Wend Finally Return Null End ' ValPolynomial(..) Private Function IsPolynomial(sInput As String) As Boolean Dim sPattern, sTerm As String Dim aResult, aTmp As New String[] Dim iI, iJ As Integer Dim sExpression As String sInput = Trim(sInput) sInput = Replace$(sInput, Left$(Format$(0, ".0")), ".") ' Alle durch + verknüpften Terme separieren aResult = Split(sInput, "+", "", True) ' While- statt For-Schleife, weil aResult in der Schleife modifiziert wird iI = 0 While iI < aResult.Count ' Zuerst das Vorzeichen am Term replizieren (-> wiederherstellen) sExpression = IIf(aResult[iI] Not Begins "-", "+", "") & aResult[iI] ' Danach wird das Polynom P(x) durch ein Array einfacher Terme ersetzt aResult.Remove(iI) ' Dann alle durch - verknüpften Terme separieren aTmp = Split(sExpression, "-", "", True) For iJ = 0 To aTmp.Max aTmp[iJ] = IIf(aTmp[iJ] Not Begins "+", "-", "") & aTmp[iJ] Next ' Abschließend tritt an die Stelle von sExpression das Array einfacher Terme aResult.Insert(aTmp, iI) iI += aTmp.Count Wend sPattern = "^[+-]?([0-9]+(\\.[0-9]+)?)?(x([\\^][0-9]+)?)?$" For Each sTerm In aResult If sTerm Not Match sPattern Then Return False Endif ' Match Pattern Next ' sTerm Return True End ' Function IsPolynomial(sInput As String) As Boolean
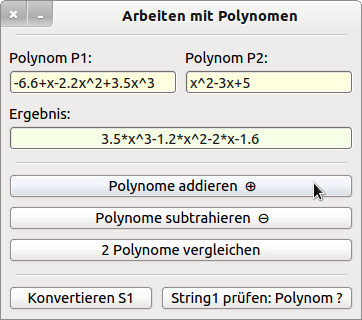
Im Beispiel werden zusätzlich die Addition, Subtraktion und der Vergleich von zwei Polynomen demonstriert :
Abbildung 29.3.4.7.1: Generieren von Polynomen
Die Funktion
Private Function ValPolynomial(sInput As String) As Polynomial ' Tobias Boege
enthält intern auch eine Prüfung (→ While hRegexp.Offset <> -1), ob die als Argument übergebene Zeichenkette als Polynom interpretiert werden kann. Das ist hier entbehrlich, weil im vorgestellten Programm nur valide Zeichenketten an diese Funktion weitergegeben werden.
Sie können die o.a. Funktion
Private Function IsPolynomial(sInput As String) As Boolean
auch durch die folgende Funktion ersetzen:
' IsPolynomial() benutzt das gleiche Verfahren wie ValPolynomial() oben. ' Es ist also nicht wesentlich schneller als der Vergleich ValPolynomial = Null. Private Function IsPolynomial(sInput As String) As Boolean sInput = Replace$(sInput, Left$(Format$(0, ".0")), ".") If Left$(sInput) Not Like "[+-]" Then sInput = "+" & sInput $hRegexp.Exec(sInput) While $hRegexp.Offset <> -1 sInput = Mid$(sInput, 1, $hRegexp.Offset) & Mid$(sInput, $hRegexp.Offset + Len($hRegexp[0].Text) + 1) If Not sInput Then Return True $hRegexp.Exec(sInput) Wend Finally Return False End ' Function IsPolynomial(..) As Boolean