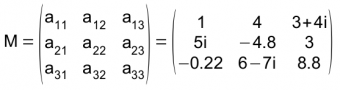Inhaltsverzeichnis
29.3.3 Klasse Matrix
Die Klasse Matrix (gb.gsl) implementiert eine zwei-dimensionale Matrix mit reellen oder komplexen Koeffizienten.
29.3.3.1 Matrix
- Eine Matrix kann als rechteckige Anordnung von unterschiedlichen mathematischen Elementen aufgefasst werden.
- Für die Klasse Matrix in Gambas sind die mathematischen Elemente entweder reelle oder komplexe Zahlen. Werden komplexe Zahlen eingesetzt, dann ist das explizit anzugeben.
- Die reellen oder komplexen Zahlen aij in einer Matrix nennt man Koeffizienten.
Hier sehen Sie die Elemente einer quadratischen Matrix mit komplexen Koeffizienten:
29.3.3.2 Eigenschaften
Die Klasse Matrix hat drei Eigenschaften:
| Eigenschaft | Datentyp | Beschreibung |
|---|---|---|
| Handle | Zeiger | Gibt einen Zeiger (Pointer) auf das interne GSL-Matrix-Objekt zurück. |
| Height | Integer | Gibt eine Dimension (Höhe = Anzahl der Zeilen) einer Matrix zurück. |
| Width | Integer | Gibt die andere Dimension (Weite = Anzahl der Spalten) einer Matrix zurück. |
Tabelle 29.3.3.2.1 : Eigenschaften der Klasse Matrix
29.3.3.3 Methoden
Die Klasse Matrix verfügt über diese Methoden:
| Methode | Rückgabetyp | Beschreibung |
|---|---|---|
| Column ( iColumn As Integer ) | Vektor | Gibt die über 'iColumn' ausgewählte Spalte einer Matrix als Vektor zurück. |
| SetColumn ( iColumn As Integer, vVector As Vector ) | - | Füllt die ausgewählte Spalte 'iColumn' einer Matrix mit den Elementen eines Vektors 'vVector'. |
| Row ( iRow As Integer ) | Vektor | Gibt die über 'iRow' ausgewählte Zeile einer Matrix als Vektor zurück. |
| SetRow ( iRow As Integer, vVector As Vector ) | - | Füllt die ausgewählte Zeile 'iColumn' einer Matrix mit den Elementen eines Vektors 'vVector'. |
| Conj ( ) | Matrix | Gibt die konjugierte Matrix zu einer gegebenen Matrix zurück. |
| Copy ( ) | Matrix | Zurückgegeben wird eine Kopie einer Matrix. |
| Inv ( ) | Matrix | Gibt die invertierte Matrix zu einer gegebenen Matrix zurück. |
| Trans ( ) | Matrix | Gibt die transponierte Matrix zur gegebenen Matrix zurück. |
| Det ( ) | Variant | Gibt die Determinante zu einer gegebenen quadratischen Matrix zurück. |
| ToString ( [ Local As Boolean ] ) | String | Zurückgegeben wird die Matrix als String-Repräsentation – in Abhängigkeit vom Parameter 'Local'. |
Tabelle 29.3.3.3.1 : Methoden der Klasse Matrix
Hinweise:
- Die Kopie einer Matrix ist ein eigenständiges Matrix-Objekt.
- Die Transponierte AT einer Matrix A entsteht, indem man die Zeilenvektoren von A als Spaltenvektoren von AT setzt. Ist A = AT, so nennt man A symmetrisch (entlang der Diagonale).
- Die Konjugierte A einer Matrix A enthält die komplex konjugierten Koeffizienten der Matrix. Ist insbesondere die Matrix A reell, ist A = A.
- Hat der Parameter Local den Wert True werden Zahlen in der lokalen Notation ausgegeben, während der Standard-Wert False den String so formatiert, dass er von der Funktion Eval(..) ausgewertet werden kann.
- Die Determinante einer Matrix kann nur für (quadratische) Matrizen berechnet werden, bei denen die Anzahl der Zeilen und gleich der Anzahl der Spalten ist.
- Der Datentyp des Funktionswertes der Methode Det() ist vom Typ Variant, weil die Determinante eine reelle Zahl oder eine komplexe Zahl sein kann.
29.3.3.4 Erzeugen einer Matrix
Es gibt unterschiedliche Möglichkeiten um Matrizen zu erzeugen:
- (A) Deklaration einer Variablen vom Daten-Typ Matrix mit impliziter Wertzuweisung.
- (B) Deklaration einer Variablen vom Daten-Typ Matrix und spätere Zuweisung der Elemente.
- (C) Kopie einer existierenden Matrix anlegen.
- (D) Verwendung der statischen Methode Matrix.Identity.
Beispiel A
Public mMatrix1 As Matrix mMatrix1 = New Matrix(3, 3, True) ' Spalten, Zeilen – komplexe Koeffizienten (alle Null) mMatrix2 = [[1, 1.4, 7 + 2i], [2, 2, 2], [-1, -2i, -3]] ' Inline-Matrix Dim Theta As Float = Pi / 2 ' Bogenmaß von 90° Dim A As Matrix = [[Cos(Theta), -Sin(Theta)], [Sin(Theta), Cos(Theta)]]
Beispiel B
Public mMatrix As Matrix Private Sub CreateAndShowMatrix() mMatrix = New Matrix(5, 5, True) ' Spalten, Zeilen mMatrix.SetRow(0, [1, 1, 1, 7 + 2i, 8]) mMatrix.SetRow(1, [2, 2, 2, 4, 5]) mMatrix.SetRow(2, [1, 0, 3, 9, 5]) mMatrix.SetRow(3, [1, 0.2, 4, 4, -3]) mMatrix.SetRow(4, [-1, -2i, -3, 4, 5 + 1i]) ' Achtung: 5 + i --> 5+1i End ' CreateMatrix()
Beispiel C
Dim cMatrix As New Matrix cMatrix = mMatrix.Copy() ' Kopie der Original-Matrix: mMatrix lblValue.Text = cMatrix.ToString(False) ' Anzeige der Elemente der Matrix-Kopie als String
Beispiel D
Auch die statische Methode Matrix.Identity erzeugt eine neue Matrix:
Static Function Identity ( [ matColumn As Integer, matRow As Integer, Complex As Boolean ] ) As Matrix
- 'matColumn' ist die die Anzahl der Spalten, zwei standardmäßig.
- 'matRow' ist die Anzahl der Zeilen, zwei standardmäßig.
- Wenn 'Complex' den Wert True hat, so können die Matrix-Koeffizienten komplexe Zahlen sein. Selbst dann, wenn Complex zunächst den Wert False hat, werden die Koeffizienten automatisch in komplexe Zahlen umgewandelt werden, wenn das erforderlich ist.
- Die Identität oder Einheitsmatrix hat außerhalb der Diagonale überall Nullen und auf der Diagonale Einsen. Nur solche Matrizen werden von Matrix.Identity() zurückgegeben.
Beispiel 1:
Public mMatrix As Matrix mMatrix = Matrix.Identity(3, 3, False) ' Reelle Koeffizienten mMatrix = [[1, 1.4, 7], [2, 2, 2], [-1, -2.88, -3]]
Beispiel 2:
Dim hMatrix As Matrix hMatrix = Matrix.Identity(5, 3, True) Print hMatrix.ToString(False)
Der Inhalt der generierten Matrix wird in der Konsole der IDE als Zeichenkette angezeigt:
[[1,0,0,0,0],[0,1,0,0,0],[0,0,1,0,0]]
29.3.3.5 Matrix-Elemente einfügen und anzeigen
In den Beispielen A und B haben Sie bereits Möglichkeiten kennengelernt, wie man Elemente in eine Matrix einfügt. Eine weitere Möglichkeit nutzt die Tatsache, dass man die Klasse Matrix wie ein Lesen-Schreiben-Array verwenden kann, dessen Elemente man auslesen oder setzen kann:
So setzen Sie ausgewählte Koeffizienten in einer Matrix:
Dim mMatrix As Matrix Dim vValue As Variant mMatrix [ iRow As Integer, iColumn As Integer ] = vValue ' Bei Array-Operationen erst Zeile, dann Spalte mMatrix[3,5] = 23.5 mMatrix[4,1] = 5-3i
Die Anzeige der Elemente einer Matrix kann zeilenweise, spaltenweise, als einzelnes Matrix-Element, als Zeichenkette oder auch komplett in einer Gitter-Komponente erfolgen.
Anzeige aller Matrix-Elemente in einer TableView:
Private Sub MatrixToTableView(aMatrix As Matrix)
Dim i, j As Integer
TableView1.Clear
TableView1.Rows.Count = aMatrix.Height
For i = 0 To aMatrix.Height - 1
For j = 0 To aMatrix.Width - 1
TableView1[i, j].Text = aMatrix[i, j]
Next ' j
Next ' i
End ' MatrixToTableView(..)
In diesem Quelltext-Abschnitt werden mehrere der o.a. Möglichkeiten der Anzeige von Matrix-Elementen demonstriert:
Private Sub ShowMatrixElements() Dim iCount, z, s As Integer ' Matrix und ausgewählte Matrix-Elemente anzeigen Print "Anzeige der Zeilen-Vektoren:\n" For iCount = 1 To mMatrix.Height ' Anzahl der Zeilen Print mMatrix.Row(icount - 1) Next ' iCount Print Print "Anzeige der Spalten-Vektoren:\n" For iCount = 1 To mMatrix.Width ' Anzahl der Spalten Print mMatrix.Column(icount - 1) Next ' iCount Print Print "Anzeige der Matrix-Elemente:\n" For z = 1 To mMatrix.Height ' Anzahl der Zeilen For s = 1 To mMatrix.Width ' Anzahl der Spalten Print mMatrix[z - 1, s - 1], Next Print Next ' iCount Print Print "Anzeige der Diagonal-Elemente (Sonderfall):\n" Print mMatrix[0, 0], Print mMatrix[1, 1], Print mMatrix[2, 2], Print mMatrix[3, 3], Print mMatrix[4, 4] Print Print "Anzeige der Matrix-Elemente in einem String:\n" Print mMatrix.ToString(False) End ' ShowElements()
Das sind die Ausgaben in der Konsole der Gambas-IDE:
Anzeige der Zeilen-Vektoren: [1 1 1 7+2i 8] [2 2 2 4 5] [1 0 3 9 5] [1 0,2 4 4 -3] [-1 -2i -3 4 5+i] Anzeige der Spalten-Vektoren: [1 2 1 1 -1] [1 2 0 0,2 -2i] [1 2 3 4 -3] [7+2i 4 9 4 4] [8 5 5 -3 5+i] Anzeige der Matrix-Elemente: 1 1 1 7+2i 8 2 2 2 4 5 1 0 3 9 5 1 0,2 4 4 -3 -1 -2i -3 4 5+i Anzeige der Diagonal-Elemente (Sonderfall): 1 2 3 4 5+i Anzeige der Matrix-Elemente in einem String: [[1,1,1,7+2i,8],[2,2,2,4,5],[1,0,3,9,5],[1,0.2,4,4,-3],[-1,-2i,-3,4,5+1i]]
29.3.3.6 Operationen und Relationen
Für Matrizen sind u.a. die folgenden Operationen erklärt: Addition, Subtraktion, Multiplikation von 2 Matrizen, Multiplikation mit einer Zahl sowie Multiplikation mit einem Vektor als Matrix-Vektor-Produkt. Im u.a. Exkurs wird auf dieses spezielle Produkt näher eingegangen. Als Relationen zwischen 2 Matrizen existieren der direkte Vergleich und die Prüfung auf Ungleichheit.
Auch ein Vergleich der String-Repräsentationen von Matrizen ist möglich:
IF GetErrorVector(aArgumente).ToString(True) = "[0 0 0 0 0 0 0]" THEN ...
29.3.3.7 Projekt
Das folgende Projekt setzt alle Varianten zur Erzeugung einer Matrix um und es wurden alle Eigenschaften und Methoden der Klasse Matrix eingesetzt.
- Vorgabe:
Es wird eine Matrix (Original) generiert, die für alle Operationen und auch bei den Relationen verwendet wird. - Die Anzeige der Original-Matrix und der Ergebnis-Matrizen erfolgt in einer (editierbaren) TableView.
- Berechnete Zahlen oder Vektoren oder Vergleichsergebnisse werden in einem Label angezeigt.
- Bei der Eingabe von komplexen Zahlen – in der allgemeinen Darstellung a+bi – muss der Wert für b explizit eingegeben werden.
- Richtig sind zum Beispiel die Darstellungen 1+1i oder 3-1i, während 3-i einen Fehler produziert. Fehleingaben zur Änderung der Koeffizienten der Originalmatrix in der TableView werden behandelt.
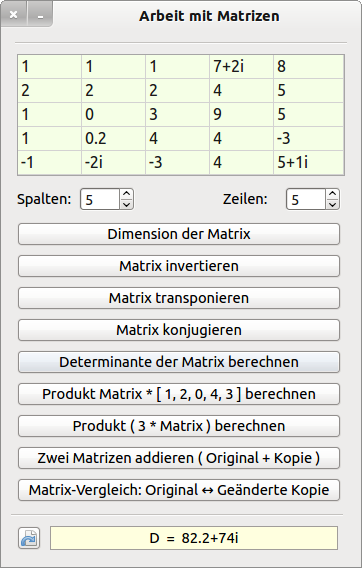
Abbildung 29.3.3.7.1: Demonstration der Arbeit mit Matrizen
Der hinreichend kommentierte Quelltext für das vorgestellte Projekt wird hier vollständig angegeben:
' Gambas class file Public mMatrix As New Matrix(5, 5, True) Public Sub Form_Open() FMain.Center() FMain.Resizable = False btnMatrixCompare.Text = "Matrix-Vergleich: Original " & String.Chr(8596) & " Geänderte Kopie" SetTableViewProperty() CreateAndShowMatrix() End ' Form_Open() Public Sub btnShowDimMatrix_Click() lblValue.Text = "Spalten: " & mMatrix.Width & " | Zeilen: " & mMatrix.Height End ' btnShowDimMatrix_Click() Public Sub btnMatrixInv_Click() Dim invMatrix As New Matrix(mMatrix.Width, mMatrix.Height, True) invMatrix = mMatrix.Inv() MatrixToTableView(invMatrix) End ' btnBetragVektorA_Click() Public Sub btnMatrixTrans_Click() Dim transMatrix As New Matrix(mMatrix.Width, mMatrix.Height, True) transMatrix = mMatrix.Trans() MatrixToTableView(transMatrix) End ' btnMatrixTrans_Click() Public Sub btnMatrixConj_Click() Dim conjMatrix As New Matrix(mMatrix.Width, mMatrix.Height, True) conjMatrix = mMatrix.Conj() MatrixToTableView(conjMatrix) End ' btnMatrixConj_Click() Public Sub btnMatrixDet_Click() If mMatrix.Height <> mMatrix.Width Then Message.Error("Die Berechnung der Determinante ist nicht möglich!<br>Die Matrix ist \ <b>nicht</b> quadratisch.") Return Else lblValue.Text = "D = " & mMatrix.Det() Endif End ' btnMatrixDet_Click() Public Sub btnMatrixMulVector_Click() Dim copyMatrix As New Matrix copyMatrix = mMatrix.Copy() ' Kopie der Original-Matrix: mMatrix lblValue.Text = copyMatrix([1, 2, 0, 4, 3]).ToString(False) End ' btnMatrixMulVector_Click() Public Sub btnMatrixMulValue_Click() MatrixToTableView(3 * mMatrix) End ' btnMatrixMulValue_Click() Public Sub btnMatrixAddMatrix_Click() MatrixToTableView(mMatrix + mMatrix.Copy()) End ' btnMatrixAddMatrix_Click() Public Sub btnMatrixCompare_Click() Dim cMatrix As Matrix cMatrix = mMatrix.Copy() cMatrix[1, 1] = 222 ' Eine Änderung an der Kopie If cMatrix = mMatrix Then lblValue.Text = "Die Matrizen sind gleich." Else lblValue.Text = "Die Matrizen sind NICHT gleich!" Endif ' cMatrix = mMatrix ? End ' btnMatrixCompare_Click() Public Sub btnReset_Click() lblValue.Text = "" CreateAndShowMatrix() ShowMatrixElements() End ' btnReset_Click() Public Sub TableView1_Save(Row As Integer, Column As Integer, ValueEdit As String) TableView1[Row, Column].Text = ValueEdit ' Zellen-Inhalt von TableView ändern If ValueEdit Not Match "[0-9][iI]" Then ValueEdit = Replace$(Replace$(ValueEdit, "i", "1i"), "I", "1I") mMatrix[Row, Column] = Eval(ValueEdit) ' Änderungen auch in Matrix übernehmen End ' TableView1_Save(..) Public Sub TableView1_Click() TableView1.Edit() End ' TableView1_Click() Private Sub CreateAndShowMatrix() mMatrix = [[1, 1, 1, 7+2i, 8],[2, 2, 2, 4, 5],[1, 0, 3, 9, 5],[1, 0.2, 4, 4, -3], [-1, -2i, -3, 4, 5+1i]] ' Matrix mit Start-Werten füllen - Alternative ' mMatrix.SetRow(0, [1, 1, 1, 7 + 2i, 8]) ' mMatrix.SetRow(1, [2, 2, 2, 4, 5]) ' mMatrix.SetRow(2, [1, 0, 3, 9, 5]) ' mMatrix.SetRow(3, [1, 0.2, 4, 4, -3]) ' mMatrix.SetRow(4, [-1, -2i, -3, 4, 5 + 1i]) ' Achtung: 5 + i --> 5+1i ' Matrix-Elemente in der TableView anzeigen MatrixToTableView(mMatrix) End ' CreateMatrix() Private Sub MatrixToTableView(aMatrix As Matrix) Dim i, j As Integer lblValue.Text = "" TableView1.Clear TableView1.Rows.Count = aMatrix.Height ' spinboxRows.Value For i = 0 To aMatrix.Height - 1 For j = 0 To aMatrix.Width - 1 TableView1[i, j].Text = aMatrix[i, j] Next ' j Next ' i End ' MatrixToTableView(..) Private Sub SetTableViewProperty() TableView1.AutoResize = True TableView1.Mode = Select.Single TableView1.Resizable = True ' Die Spaltenbreite kann mit der Maus geändert werden TableView1.AutoResize = True ' Die letzte Spalte verfügt über vorhandene (Rest-)Breite TableView1.Background = &HF5FFE6 ' hellgrün TableView1.NoKeyboard = False ' Wenn TRUE, dann Pfeiltasten OHNE Wirkung zum Navigieren in Gitter-Spalten TableView1.Rows.Count = mMatrix.Height TableView1.Columns.Count = mMatrix.Width End ' SetTableViewProperty()
29.3.3.8 Exkurs
(A)
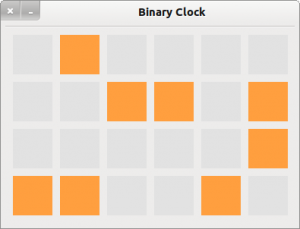
Im Kapitel '20.3.1.3 Beispiel 3 – Uhr mit binärer Anzeige' wird eine binäre Uhr vorgestellt:
Abbildung 29.3.3.8.1: Uhr mit binärer Anzeige
Die rechteckige Anordnung der Bits lässt sich leicht auf eine Matrix als Datenstruktur abbilden – wie der folgende Quelltext-Ausschnitt zeigt:
Public Function SetTimeMatrix() As Matrix Dim iRow, iColumn As Integer Dim sZeitHMS As String Dim vTime As New Vector(6, False) Dim mBitMatrix As New Matrix(6, 4, False) sZeitHMS = Replace(Str(Time(Now())), ":", "") For iRow = 1 To mBitMatrix.Height ' 6 vTime[iRow - 1] = Mid(sZeitHMS, iRow, 1) For iColumn = 1 To mBitMatrix.Width ' 4 mBitMatrix[iRow - 1, iColumn - 1] = Mid(Str(Bin(vTime[iRow - 1], 4)), iColumn, 1) Next ' iColumn Next ' iRow Return mBitMatrix End ' Function SetTimeMatrix()
(B)
Die Klasse Matrix kann auch wie eine Funktion benutzt werden:
Function Matrix( vector As Vector ) As Vector
Die Matrix wird mit einem Vektor vector multipliziert und liefert als Produkt einen Vektor:
Public Sub MatrixMulVector(aMatrix As Matrix, aVector As Vector) Dim vResult As Vector vResult = aMatrix(aVector) ' Matrix-Vektor-Produkt lblValue.Text = vResult.ToString(False) ' Anzeige des Ergebnisvektors als String ' lblValue.Text = aMatrix(aVector).ToString(False) ' Verzicht auf die lokale Variable vResult End ' btnMatrixMulVector_Click() Public Sub btnTest_Click() MatrixMulVector(mMatrix, [1, 2, 0, 4, 3]) End
Der Ergebnisvektor mit der Matrix mMatrix aus dem o.a. Projekt ist: [ 55+8i, 37, 52, 8.4, 30-1i ].
Hier folgt ein Beispiel, bei dem Vektoren in der Ebene über ein (Dreh-)Matrix-Vektor-Produkt um 90° gedreht werden können:
Public Sub Main() Dim Theta As Float = Pi / 2 ' Bogenmaß von 90° als reelle Zahl Dim A As Matrix = [[Cos(Theta), -Sin(Theta)], [Sin(Theta), Cos(Theta)]] ' A ist eine so genannte Dreh-Matrix ' Wird ein Vektor v von rechts an A multipliziert, dreht A den Vektor um den Winkel Theta=Pi/2, d.h. 90° ' A(v) ist das nicht-kommutative Matrix-Vektor-Produkt A*v. Print A([1, 0]) Print A([0, 1]) End ' Main