Im diesem Projekt von Tobias Boege wird eine Hilbert-Kurve beliebiger Ordnung gezeichnet – zumindest theoretisch. Praktisch können Sie noch Kurven bis zur Ordnung 8 oder 9 auf einem normalen Monitor sehen.

Abbildung 23.3.5.8.1: Hilbert-Kurve 6. Ordnung

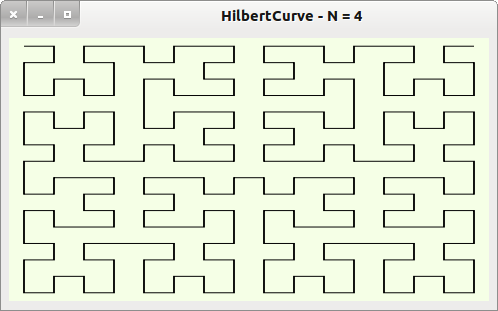
Das Programm startet mit einer Hilbert-Kurve der Ordnung 4. Mit den Tasten „+“ und „-“ können Sie die Ordnung ändern.

Abbildung 23.3.5.8.2: Start-Kurve mit N=4

Der Projekt-Quelltext ist sehr kurz und zeigt den Einsatz von Methoden der Klasse Paint – insbesondere von Paint.Scale() und Paint.Translate(). Es wird gezeigt, wie man Funktionen schreibt, die vom aktuellen Paint-Device unabhängig sind, denn mit den Funktionen im Projekt kann man sowohl auf eine DrawingArea als auch auf ein Picture zeichnen, ohne etwas zu ändern.

Der Quelltext liest sich etwas schwerer, weil in der Prozedur _HilbertKurve(…) zum Teil rekursiv programmiert wird und der Quelltext somit sehr kompakt wird.

' Gambas class file
 
Private $iOrder As Integer = 4
Private $iX As Integer
Private $iY As Integer
 
Public Sub Form_Open()
  FMain.Center
  FMain.Height = (9 / 16) * FMain.Width
End
 
Public Sub Form_KeyPress()
  If Key.Code = Key["+"] Then
    Inc $iOrder
    dwgKurve.Refresh()
  Else If Key.Code = Key["-"] And If $iOrder > 0 Then
    Dec $iOrder
    dwgKurve.Refresh()
  Endif
 
End
 
Public Sub dwgKurve_Draw()
  $iX = 0
  $iY = 0
  Inc Application.Busy
    FMain.Title = "HilbertCurve - N = " & $iOrder 
    HilbertCurve($iOrder)
  Dec Application.Busy
End
 
Private Sub HilbertCurve(Order As Integer)
  With Paint.Device
    Paint.Scale(.W / 2 ^ Order, .H / 2 ^ Order)
    Paint.Translate(0.5, 0.5)
    Paint.LineWidth = 2 ^ Order / Min(.W, .H)
  End With
  _HilbertCurve(0, 1, Order)
  Paint.Stroke()
End
 
' Found in Warren, Henry S. Jr.: Hacker's Delight. 2nd ed. Addison-Wesley (2013), pp. 356ff.
' The routine is attributed to Voorhies, Douglas: Space-Filling Curves and a Measure of Coherence.
' Graphics Gems II, AP Professional (1991).
 
Private Sub _HilbertCurve(Direction As Integer, Rotation As Integer, Order As Integer)
  If Order = 0 Then Return
 
  Direction += Rotation
  _HilbertCurve(Direction, - Rotation, Order – 1) ' Rekursion 1
  _HilbertStep(Direction)
 
  Direction -= Rotation
  _HilbertCurve(Direction, Rotation, Order - 1) ' Rekursion 2
  _HilbertStep(Direction)
  _HilbertCurve(Direction, Rotation, Order - 1) ' Rekursion 3
 
  Direction -= Rotation
  _HilbertStep(Direction)
  _HilbertCurve(Direction, - Rotation, Order - 1) ' Rekursion 4
End
 
Private Sub _HilbertStep(Direction As Integer)
  Select Case Direction And 3
    Case 0
      Inc $iX
    Case 1
      Inc $iY
    Case 2
      Dec $iX
    Case 3
      Dec $iY
  End Select
  Paint.LineTo($iX, $iY)
End