Inhaltsverzeichnis
11.5.2 Fehler-Prävention
In diesem Kapitel geht es darum, auf mögliche Fehlerquellen beim Programmieren hinzuweisen. Diese Hinweise sollen Ihnen helfen, die den Programmen zugrunde liegenden Algorithmen möglichst fehlerfrei in Gambas-Quelltext umzusetzen. Die Hinweise sind vielfältig und widerspiegeln die Bandbreite potenzieller Fehlerquellen.
11.5.2.1 Erfahrungen nutzen
Es hat sich generell als hilfreich erwiesen, zu bestimmten Themen im Archiv der (englischen) Mailing-Liste nachzusehen, um auf den Erfahrungsschatz der anderen Gambas-Programmierer zurückzugreifen oder über Neuigkeiten informiert zu werden. So werden Sie fündig:
Syntax: https://lists.gambas-basic.org/cgi-bin/search.cgi?q=suchliste_eintrag_getrennt_durch_+ Beispiel: https://lists.gambas-basic.org/cgi-bin/search.cgi?q=picturebox+clear
Was Neuerungen in Gambas betrifft gilt: Auf die Einträge in der Mailingliste achten und die 'Release Notes' lesen ist momentan der einzig verlässliche Weg, um gut informiert zu sein, da die Veröffentlichungen in der Dokumentation leider nicht zeitnah erfolgen!
11.5.2.2 Gambas Release Notes – Changelog
Sie ersparen sich Kummer, nicht nur mit älteren Gambas-Projekten, wenn Sie sich die veröffentlichten Änderungen wie in http://gambaswiki.org/wiki/doc/release/3.12.2nh in neuen Gambas-Versionen genau durchlesen. Dann wären Sie zum Beispiel informiert, dass der u.a. Quelltext *** ab der Gambas-Version 3.12.2 so nicht mehr erlaubt ist! Davor war es möglich, eine globale Variable zu deklarieren, um sie auf diese Weise zu verwenden:
Private hControl As Control ' *** Public Sub Form_Open() For Each hControl In Me.Controls Print hControl.Name Next End
Korrekt ist ab Gambas-Version 3.12.2 dieser Quelltext:
Public Sub Form_Open()
Dim hControl As Control
For Each hControl In Me.Controls
Print hControl.Name
Next
End
Beachten Sie, dass Laufvariablen in Kontrollstrukturen lokale Variablen sein müssen! Sonst erhalten Sie eine Fehlermeldung wie 'Loop variable cannot be global in FMain.class:33'. Das hat auch zur Folge, dass Sie den Quelltext in Ihren älteren Projekten u.U. anpassen müssen!
Die folgenden Ankündigungen in Gambas 3.12.2 brachten nur Erweiterungen und Ergänzungen in Gambas, die Sie kennen sollten – Fehler ergeben sich aber nicht, wenn Sie diese Neuerungen nicht verwenden. Sie sind aber im Vorteil, weil Sie dann Quelltext verstehen, der diese Erweiterungen und Ergänzungen einsetzt.
- Local variables can now be declared anywhere in the function body.
- FOR and FOR EACH syntax now can declare their loop variables.
- String can now be accessed with the array syntax.
Der folgende Quelltext ist korrekt:
[1] ' Gambas class file [2] [3] Public Sub btnTest_Click() [4] [5] Dim sString As String [6] [7] sString = "Gambas" [8] Print "sString = "; [9] For iCount As Integer = 0 To sString.Len – 1 [10] Print sString[iCount]; [11] Next [12] Print [13] [14] Dim aString As String[] [15] [16] aString = ["G", "a", "m", "b", "a", "s"] [17] Print "aString = ["; [18] For iCount As Integer = 0 To aString.Count – 1 [19] Print aString[iCount]; [20] Next [21] Print "]" [22] [23] Dim i As Integer = 1 [24] [25] While i < 10 [26] i = i * 2 [27] Wend ' i ist 16 = 2^4 [28] [29] Dim j As Integer = i ^ 2 ' 16^2 = 256 [30] Print j [31] [32] End
Das sind die Ausgaben in der Konsole der IDE:
sString = Gambas aString = [Gambas] 256
Kommentar
- Die Deklarationen in den Zeilen 5, 14, 23 und 29 sind zulässig. An der Vorgabe: „Eine Variable kann erst dann verwendet werden, nachdem sie deklariert wurde“ ändert das nichts!
- In den Zeilen 9 und 18 werden die lokalen Variablen iCount innerhalb der Kontrollstruktur deklariert. Die Verwendung gleicher Bezeichner für die so genannten Laufvariablen ist zulässig.
- Der Hinweis „Auf Zeichenketten kann nun mit der Array-Syntax zugegriffen werden.“ muss relativiert werden. Offensichtlich ist nur die Möglichkeit gemeint, über den Index mit String[index] auf die einzelnen Zeichen zuzugreifen. Hinter einem nativen String steht jedoch keine Klasse und daher existieren keine Methoden wie String.Count. Es ist zu vermuten, dass es sich beim Array-Zugriff auf Strings um einen Hack im Compiler handelt, der diese Syntax zulässt und speziell behandelt.
- In der Zeile 29 wird die Variable j tatsächlich mit einem Wert initialisiert, der von den der Deklaration vorangehenden Berechnungsschritten in den Zeilen 25 bis 27 abhängt. Die Variable j ist erst unterhalb ihrer Deklaration verfügbar.
11.5.2.3 Gambas-Konventionen
Die genaue Kenntnis der folgenden Gambas-Konvention lässt Sie einen (unbekannten) Quelltext besser verstehen und beugt Fehlern in eigenen Quelltexten vor. So gilt:
Wenn eine (boolsche) Funktion (Dialog) nach einer Aktion benannt ist (Connect, Close, …), dann gibt sie bei Erfolg `False` und bei Misserfolg `True` zurück. Ist die Methode (oder Eigenschaft) nach einem Attribute benannt (IsEmpty, IsVector, …), dann ist der Rückgabewert dem Namen entsprechend.
Beispiel 1
Ein Musterbeispiel ist die Methode Dialog.Open(). Diese Methode ist nach einer Aktion benannt (Open) und gibt False zurück, wenn eine Datei erfolgreich zum Öffnen ausgewählt wurde:
If Dialog.Open() Then Return ' Sie können jetzt die Eigenschaft Dialog.Path verwenden ...
Wenn der Rückgabewert von Dialog.Open() gleich True ist – das ist der Fehlerfall (!) – dann sollte der Dialog mit Return abgebrochen werden. Sonst können Sie die Eigenschaft Dialog.Path verwenden.
Beispiel 2
Private Function IsVector(sInput As String) As Boolean Dim sSubject, sPattern As String sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Not Match sPattern Then Return False ' Fehler Return True ' Erfolg End
Diese Funktion – benannt nach dem Attribut IsVector – gibt wie erwartet für den Erfolg `True` und bei Misserfolg `False` zurück.
Diese o.a. Konventionen müssen Sie nicht nach Logik oder Sinnhaftigkeit beurteilen. Sie müssen diese nur kennen und beachten! Somit sind sie ein Teil des Programmierparadigmas von Gambas. Verwenden Sie in Ihren Projekten eigene Konventionen, dann können Sie das tun. Nur fällt es dann anderen Programmierern schwer, den Quelltext zu verstehen oder zu verwenden. Fehler sind dann – im wahren Sinne des Wortes – vorprogrammiert.
Zu diesem Themenkreis gehören auch die Umwandlungen von Wahrheitswerten `True und `False` in numerische Werte:
Dim bComparisonA, bComparisonB As Boolean bComparisonA = (8 > 5) bComparisonB = (Pi() = 355 / 113) Print CBoolean(bComparisonA) Print CString(CInt(bComparisonA)) Print CBoolean(bComparisonB) Print CString(CInt(bComparisonB))
Das sind die Ausgaben in der Konsole der IDE:
True -1 False 0
11.5.2.4 Numerik – Zahlenvergleiche, Rundungsfehler und Überlauf
Auf dieser Seite: http://gambaswiki.org/wiki/cat/float finden Sie interessante Details zu den Gleitkommazahlen.
Beispiel 1: Zahlen-Vergleiche in der Art If a = b Then … sollten Sie vermeiden. Besser ist es, wenn Sie nach einer Umformung If (a-b) = 0 Then … eine Epsilon-Umgebung |a − b| < ε mit ε ∈ ℝ und ε > 0 nutzen:
Public fEpsilon As Float fEpsilon = 0.0001 If Abs(a-b) < fEpsilon Then ...
Die Begründung für dieses Vorgehen liegt darin, dass die Computerzahlen diskret sind, bei den Rechnungen Rundungsfehler entstehen (können) und sich diese aufsummieren.
Das Beispiel 2 zeigt unterschiedliche Ergebnisse für die gleiche Berechnung mit unterschiedlich ge-rundeten Ergebnissen:
~ $ gbx3 -e "tan(rad(45))-1" ' Erwartet wird Null > -1,11022302462516E-16 ~ $ gbx3 -e "round(tan(rad(45))-1,-1)" > 0 ~ $ gbx3 -e "round(tan(rad(45))-1,-15)" > 0 ~ $ gbx3 -e "round(tan(rad(45))-1,-16)" > -1E-16
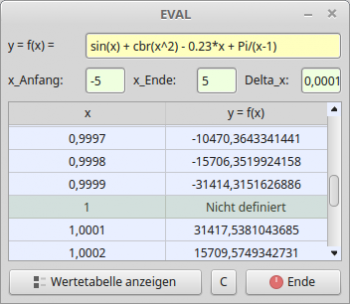
Beispiel 3: Bei der Berechnung der Wertetabelle der Funktion f(x) = sin(x) + cbr(x^2) - 0.23*x + Pi/(x-1) im Intervall -5 ≤ x ≤ +5 gab es bereits bei kleinen Schrittweiten ∆x Fehler in der Form, dass es für die Polstelle xp = 1 nicht den erwarteten Text 'Nicht definiert' ergab. Dieser Text wird ausgegeben, wenn für ein bestimmtes Argument kein Funktionswert berechnet werden kann:
∆x x f(x) ------------------------------------------------- 0,1 1 -2,82969510081138E+16 0,01 0,99999999999994 -5,09854973119151E+13 0,001 1 +4,7161585013523E+15 ------------------------------------------------- Tabelle 1
Eine wesentliche Verbesserung ergibt sich, wenn die Schrittweite ∆x als Zweier-Potenz mit 2^k und k ∈ {-1,-2,..,-9,-10,-11} gewählt wird:
∆x x f(x) ------------------------------------------- 1/2 1 Nicht definiert 1/4 1 Nicht definiert 1/8 1 Nicht definiert ... 1/512 1 Nicht definiert ... 1/4096 1 Nicht definiert ------------------------------------------- Tabelle 2
Die Verbesserung kann man aus dem IEEE-754-Standard [https://de.wikipedia.org/wiki/IEEE_754] für die Darstellung von Gleitkommazahlen ableiten. Danach können Sie jede reelle Zahl z darstellen als
z = σ⋅m⋅2^e
wobei σ das Vorzeichen +1 oder -1 ist, m die sogenannte Mantisse und e der Exponent. Eine Zahl vom Typ Float wird als Tripel (σ,m,e) abgespeichert. Da nur 64 Bits zur Verfügung haben, müssen diese 64 Bits auf Vorzeichen σ, Mantisse m und Exponent e aufgeteilt werden. Nach dem IEEE-754-Standard gilt die Festlegung: σ benötigt genau 1 Bit, m bekommt 52 Bits und e die restlichen 11. Sie erkennen, dass Zahlen z mit ±2^e exakt abgespeichert werden können, solange der Exponent in seinen 11 Bits bleibt, also zwischen -1022 und 1023 liegt. Außerdem ist die Addition von diesem z auf eine Zahl vom Typ Float exakt, wenn die Exponenten nah genug beieinander liegen.
Fazit: Zweierpotenzen können korrekt abgespeichert werden. Das macht sie besser für Schrittweiten geeignet als etwa 1/10, dessen Speicherung allein schon inhärent Rundungsfehler verursacht, wie es das folgende Beispiel Zahl z = 0.1; Datentyp Single (32-Bit-Darstellung) zeigt:
Zahl: 0.1 Single: 0.100000001490116119384765625 Fehler: 1.490116119384765625E-9 Binär: 00111101110011001100110011001101 Hex: &H3DCCCCCD Zahl: 0.0001220703125 = 1/8192 = 2^(-13) Single: 0.0001220703125 Fehler: 0 Binär: 00111001000000000000000000000000 Hex: &H39000000
Eine weitere Verbesserung wird durch die Umsetzung der folgenden Überlegungen erreicht. In der Funktion zur Berechnung des Funktionswertes stand in der ersten Version:
Repeat ' ... x += Me.DeltaX Until x >= Me.EndX
Damit werden im Argument x Rundungsfehler aufsummiert, weil mit x += Me.DeltaX jede einzelne Addition fehlerbehaftet ist. Genau das führt zu den Werten in der Tabelle 1.
Es ist besser, wenn Sie das Argument x in jeder Iteration so neu berechnen:
i = 0 Repeat ' ... Inc i x = Me.StartX + i * Me.DeltaX Until x >= Me.EndX
Die erzielten Ergebnisse bei der Berechnung des Funktionswertes für unterschiedliche Schrittweiten ∆x sind überzeugend:
∆x x f(x) ------------------------------------------- 0,1 1 Nicht definiert 0,01 1 Nicht definiert 0,001 1 Nicht definiert 0,0001 1 Nicht definiert ------------------------------------------- Tabelle 3
Abbildung 11.5.2.4.1: Wertetabelle für f(x)
11.5.2.5 Überlauf abfangen
Public Const MinFloat As Float = -8.98846567431105E+307 Public Const MaxFloat As Float = +8.98846567431105E+307 With aValuePair grdData[i,0].Text = Str(.X) grdData[i,1].Text = If(.Valid,If((.Y < MinFloat) Or (.Y > MaxFloat),"Überlauf",Str(.Y)), "nicht definiert") End With
Wenn Sie die Formatfunktion Format$(…) für die Ausgabe verwenden, müssen Sie auf die Exponentialdarstellung verzichten. Das aber kann zu unsinnigen Ausgabewerten führen, weil Ihnen ein Überlauf dann nicht angezeigt wird. Wenn Sie in einem Programm mit vielen Berechnungen einen Overflow-Fehler [http://gambaswiki.org/wiki/error/overflow] erhalten, dann bedeutet das: Der Interpreter hat festgestellt, dass das Ergebnis einer Berechnung zu groß ist. Auch der JIT-Compiler führt Überlaufprüfungen durch.
Beispiel 1: Dieser Fehler tritt auf, wenn eine Zahl fFL vom Typ Float oder Long in eine Zahl vom Typ Single konvertiert wird, aber die Zahl fFL zu groß ist:
~ $ gbx3 -e 'CStr(CSingle(2 ^ 500))' > Overflow
Beispiel 2: Dieser Fehler tritt auf, wenn die Arithmetik mit Datumsangaben einen Wert mit mehr als 32 Bit erzeugt:
~ $ gbx3 -e 'CStr(DateDiff(CFloat(2 ^ 50), CFloat(1), gb.Second))' > Overflow
11.5.2.6 Valide Daten
Als Programm-Entwickler sollten Sie dafür Sorge tragen, dass in Ihren Programmen nur valide Daten verarbeitet werden, um Laufzeitfehler zu verhindern. Die zu verarbeitenden Daten stammen dabei aus sehr unterschiedlichen Daten-Quellen. Sie werden
entweder über (externe) Datenspeicher eingelesen oder in Echtzeit von Sensoren über geeignete Interfaces bereitgestellt oder entstehen als (temporäre) Daten - zum Beispiel als Ergebnis von Berechnungen - zur Laufzeit des Programms oder werden aus geeigneten Steuer-Elementen wie zum Beispiel TextBox oder ValueBox über eine Tastatur eingegeben oder mit der Maus zum Beispiel aus einer Spinbox ausgewählt. Anschließend werden sie in den erforderlichen Datentyp konvertiert sowie abschließend validiert.
Im Kapitel `6.6.2 Valide Daten` werden Ihnen viele Wege zu validen Daten ausführlich beschrieben.
11.5.2.7 Automatische Typumwandlung
Hätten Sie die Ergebnisse in der Ausgabe der Konsole in der IDE so erwartet:
Dim s As String = "44"
Print "Typ = "; TypeOf(3 * s); " ▸ "; 3 * s
Print "Typ = "; TypeOf(True); " ▸ "; True
Print "Typ = "; TypeOf("10"); " ▸ "; "10"
Print "Typ = "; TypeOf(Pi(2)); " ▸ "; Pi(2)
Print "Typ = "; TypeOf(Now()); " ▸ "; Now()
Print "Typ = "; TypeOf(Date(Now())); " ▸ "; Format$(Date(Now()), "dd.mm.yyyy")
Print "Typ = "; TypeOf(Day(Now())); " ▸ "; Day(Now())
Print "Typ = "; TypeOf(CString(3 * CInteger(s))); " ▸ "; CString(3 * CInteger(s))
Ausgabe in der Konsole der IDE:
> Typ = 7 ▸ 132 ' Float > Typ = 1 ▸ True ' Boolean > Typ = 9 ▸ 10 ' String > Typ = 7 ▸ 6,28318530717959 ' Float > Typ = 8 ▸ 01.04.2019 20:03:03 ' Date > Typ = 8 ▸ 01.04.2019 ' Float > Typ = 4 ▸ 1 ' Integer > Typ = 9 ▸ 132 ' String
Das Bemerkenswerte bei allen Ausgaben ist, dass sie offensichtlich alle (automatische) Konvertierungen in den Datentyp String sind, denn die Anweisung Print gibt nur Zeichenketten aus! Erstaunt es Sie, dass sogar eine Multiplikation von einer Integer-Zahl mit einem String, der eine Integer-Zahl enthält, akzeptiert wird - aber das Produkt 3*s vom Typ Float ist?
Bei ähnlichen Konvertierungen wie mit x und y als Gleitkommazahlen (Datentyp Float) finden drei Konvertierungen von Float nach String statt:
Dim x, y As Float
x = Round(Pi(3), -4)
y = 10.0
Print x & " - " & y & " = " & (x - y)
Print Subst$("&1 - &2 = &3", x, y, x - y) ***
> 9.4248 - 10 = -0.5752
Die Ausgabe *** liefert das gleiche Ergebnis, ist aber der oberen Print-Anweisung vorzuziehen. Diese hat den Vorteil, dass solche String-Templates wie „&1 - &2 = &3“ besser in andere Sprachen übersetzbar sind, was mit mehrfacher Konkatenation von Strings nicht immer gut gelingt. Außerdem ist gut erkennbar, dass eine Differenz von 2 Operanden ausgegeben werden soll. Kleiner Hinweis - nicht nur am Rande: Die Print-Anweisung benutzt intern nicht CString(), sondern die Methode Str$(). Im Terminal sehen Sie also immer die locale-behafteten Ausgaben von Daten!
11.5.2.8 Explizite Typumwandlung
Bei expliziten Typ-Umwandlungen sind Aspekte der Lokalisierung (Locale) zu beachten. Nach Wikipedia (https://de.wikipedia.org/wiki/Locale) gilt: „Das Locale ist ein Einstellungssatz, der die Gebietsschemaparameter (Standortparameter) für Computerprogramme enthält. Dazu gehören in erster Linie die Sprache der Benutzeroberfläche, das Land und Einstellungen zu Zeichensatz, Tastaturlayout, Zahlen-, Währungs-, Datums- und Zeitformaten. Ein Einstellungssatz wird üblicherweise mit einem Code, der meist Sprache und Land umfasst, eindeutig identifiziert.“. Gambas benutzt die (System-)Locale der Standardbibliothek (GLib).
Bei der Validierung von Datumsangaben oder numerischen Werten, der Konvertierung zwischen Datumsangaben oder numerischen Werten und Strings kommt das zum Tragen. Es gibt zwei Ebenen von Konvertierungsfunktionen:
1. Die untere Ebene enthält die Funktionen wie CInt(), CFloat() oder CString() – beschrieben in der Dokumentation unter http://gambaswiki.org/wiki/cat/conv. Die Funktionen der unteren Ebene berücksichtigen die aktuelle Locale nicht. Sie sollten verwendet werden, wenn Sie zum Beispiel eine Zahl als String in einer Datei abspeichern und später wieder als Zahl einlesen wollen.
2. Die obere Ebene besteht aus den Funktionen Val$(), Str$() und Format$(). Diese Funktionen berücksichtigen die aktuelle Locale. So wird eine Zahl zum Beispiel mit dem korrekten Dezimal-trennzeichen oder die Komponenten einer Datumsangabe nach der in der aktuellen Locale gebräuchlichen Reihenfolge und den passenden Trennzeichen formatiert. Diese Ebene ist für die Anzeige von Daten beim Benutzer gedacht.
11.5.2.8.1 Validierung Zahlenwerte – Punkt oder Komma - das ist hier die Frage
Die Antwort wird nur dann von Bedeutung sein, wenn Sie dem Benutzer die Möglichkeit eröffnen, reelle Zahlen entsprechend seiner Locale zum Beispiel in eine Textbox einzugeben und auch dort anzuzeigen. Wollen Sie aber, dass konsequent das englische Zahlen-Format mit einem Punkt als Dezimal-trennzeichen benutzt werden soll, dann verwenden Sie die Funktionen CFloat(Expression AS Variant) für das Konvertieren des eingelesenen Strings in eine Gleitkommazahl vom Datentyp Float und die Funktion CString(Expression AS Variant) für das Konvertieren der Gleitkommazahl in einen String. Beachten Sie:
Gambas-intern wird immer mit dem englischen Zahlenformat für Gleitkommazahlen gearbeitet. In einer deutschen Locale ist das Dezimaltrennzeichen ein Komma und der Punkt das Tausender-Trennzeichen bei der Gliederung von Zahlen in Zifferngruppen (Dreigruppe). In einer englischen Locale ist das Dezimaltrennzeichen ein Punkt und das Komma Tausender-Trennzeichen bei der Gliederung von Zahlen in Zifferngruppen (Dreigruppe).
Fall 1 - Englisches Zahlen-Format
Es soll eine Gleitkommazahl (Datentyp Float) über eine Textbox im englischen Zahlen-Format eingegeben werden und das Ergebnis interner Berechnungen in einer weiteren Textbox im gleichen Zahlen-Format angezeigt werden. Die aktuelle Locale wird nicht berücksichtigt! Die Lösung zeigt sich im folgenden Quelltext:
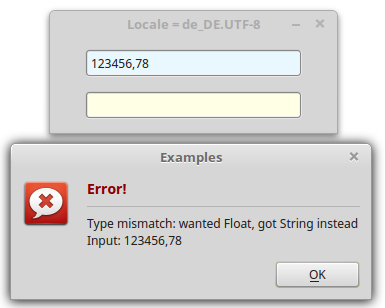
Public Sub TextBox1_Activate() Dim fValue, fResult As Float Dim sMessage As String Try fValue = CFloat(TextBox1.Text) If Error Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= Error.Text & "<br>" sMessage &= "Input: " & TextBox1.Text Message.Error(sMessage) Else fResult = Round(fValue * Pi(3.66), -3) TextBox2.Text = CString(fResult) Endif End
Abbildung 11.5.2.8.1: Englisches Zahlenformat – unabgängig von der Locale
Abbildung 11.5.2.8.2: Englisches Zahlenformat – unabgängig von der Locale
Fall 2 - Lokales Zahlen-Format
Im Gegensatz zum 1. Fall soll die aktuelle Locale berücksichtigt werden! Der Quelltext nutzt aus diesem Grund andere Funktionen zum Validieren und Konvertieren (String ↔ Zahl und Zahl ↔ String):
Public Sub TextBox1_Activate() Dim fValue, fResult As Float Dim sMessage As String If Not IsFloat(TextBox1.Text) Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= "No floating-point number - related to the current locale." Message.Error(sMessage) Else fValue = Val(TextBox1.Text) fResult = Round(fValue * Pi(3.66), -3) TextBox2.Text = Str$(fResult) Endif End
Kommentar
- Beachten Sie, dass die Datentyp-Funktionen - anders als beispielsweise CFloat() - niemals einen Fehler auslösen, was deshalb ein Konstrukt aus Try und If Error entbehrlich macht.
- Alternativ können Sie für Str$() auch die Format-Funktion Format$() einsetzen.
- Im Deutschen gilt auch „123.456“ als Gleitkommazahl, aber „123.45“ nicht, weil das Tausender-Trennzeichen wegen der fehlenden Dreiergruppe nicht als solches erkannt wird.
- Die Prüfung mit IsFloat(…) vor der Konvertierung mit Val(…) ist notwendig, wie Sie an folgendem Beispiel sehen:
$ LC_NUMERIC=de_DE.utf8 gbx3 -e 'Str(Val("1.2"))'
> 01.02.2019 00:00:00
Exkurs
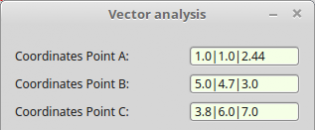
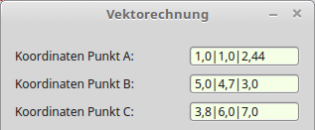
Für ein Projekt zur Vektorrechnung sollten in Abhängigkeit von der aktuellen Locale spezielle Vorgabewerte beim Programmstart in eine Textbox eingegeben werden:
Abbildung 11.5.2.8.3: Vorgabewerte in Abhängigkeit von der aktuellen Locale
Die Realisierung ist einfach, denn es wird das in der aktuellen Locale genutzte Dezimaltrennzeichen ermittelt und berücksichtigt:
Public Sub Form_Open() ... Init() ... End Private Sub Init() If Left$(Format$(0, ".0")) = "," Then txbInputA.Text = "1,0|1,0|2,44" txbInputB.Text = "5,0|4,7|3,0" txbInputC.Text = "3,8|6,0|7,0" Else txbInputA.Text = "1.0|1.0|2.44" txbInputB.Text = "5.0|4.7|3.0" txbInputC.Text = "3.8|6.0|7.0" Endif End
Um Eingabefehlern in den Textboxen vorzubeugen können Sie für die Eingaben ein Eingabe-Alphabet vorgeben und das locale-bewusst einsetzen. Im angegebenen Fall werden alle drei TextBoxen zu einer Gruppe zusammengefasst:
Private Sub CheckInput(sAllowed As String) ' Idee: Charles Guerin Select Case Key.Code Case Key.Left, Key.Right, Key.BackSpace, Key.Delete, Key.End, Key.Home, Key.Enter, Key.Return Return Default If Key.Text And If InStr(sAllowed, Key.Text) Then Return Endif End Select Stop Event End Public Sub TBGroup_KeyPress() ' Gilt für die *TextBox-Gruppe* TBGroup! If Left$(Format$(0, ".0")) = "," Then CheckInput("+-,|0123456789") Else CheckInput("+-.|0123456789") Endif End
Auf die Validierung der Eingabe können Sie nicht jedoch nicht verzichten. Mit der folgenden Funktion ist das kein Problem:
Private Function IsVector(sInput As String) As Boolean Dim sSubject, sPattern As String sSubject = sInput sSubject = Replace(sSubject, " ", "") sSubject = Replace$(sSubject, ",", ".") sPattern = "^([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+[|])([-+]?[0-9]*\\.?[0-9]+)$" If sSubject Not Match sPattern Then Return False Return True End
11.5.2.8.2 Datum und Gleitkommazahlen
Der Funktionswert der Funktion Now() repräsentiert das aktuelle Datum. Dieser Datumswert wird intern in Gambas auf eine Gleitkommazahl vom Datentyp Float abgebildet. Die Float-Darstellung eines Datums ist nicht vollständig dokumentiert. In der Dokumentation zur Funktion Frac(…) in http://gambaswiki.org/wiki/lang/frac gibt es einen Hinweis darauf. Das Datum wird in der Gleitkommazahl durch den ganzzahligen Anteil beschrieben und die Zeit durch den gebrochenen Anteil:
Print Now() Print "Datum Σ: "; CFloat(Now()) Print "Datum: "; CInt(Now()) Print "Zeit: "; Round(Frac(Now()), -8)
04.04.2019 19:19:10 Datum Σ: 2490682,72164661 Datum: 2490682 Zeit: 0,72164661
Der ganzzahlige Anteil repräsentiert die Anzahl der Tage seit einem bestimmten Zeitpunkt, den man als Beginn des „Gambas-Kalenders“ bezeichnen kann. Erinnern Sie sich, dass der 1.1.1970 als Beginn des UNIX-Kalenders gilt, weil die herkömmlichen Zeitstempel auf UNIX-artigen Systemen die Sekunden seit diesem Datum zählen? Der Gambas-Kalender dagegen beginnt mit dem Jahr 4801 v. Chr. wie die folgende Ausgabe zeigt:
$ gbx3 -e 'CString(CDate(1))' 01/01/-4801
In der Gambas-Dokumentation [http://gambaswiki.org/wiki/lang/time] findet sich aber die Aussage, dass der gregorianische Kalender kein Jahr 0 kennt. In Gambas wird das Jahr 0 dafür verwendet, um Datumswerte zu kennzeichnen, die nur einen Zeit-Teil haben.
Nun zur Zeit: Der gebrochene Anteil ist eine Gleitkommazahl vom Datentyp Float im halboffenen Intervall [0,1). Sie beschreibt die Tageszeit als Anteil der 24 Stunden eines Tages. So entspricht ein Zeit-Teil zum Beispiel von 0.5 einer Tageszeit von Punkt 12 Uhr:
$ gbx3 -e 'CString(CDate(0.5))' 12:00:00
Es ist unbekannt, ob man bei Datumsangaben den auftretenden (Float)-Rundungsfehlern Beachtung schenken muss. Einerseits kann man eine Zeit wie 8:00 Uhr nicht exakt darstellen, weil es für 1/3 (eines Tages) keine exakte Binärdarstellung gibt. Andererseits ist die Float-Approximation weit über die Nanosekunden hinaus genau.
$ gbx3 -e 'CString(CDate(1/3))' 08:00:00 Print CString(CFloat(Time(8, 0, 0))) > 0.33333333333333
Somit ist die Abbildung eines Datums auf eine Gleitkommazahl vom Datentyp Float eine clevere Idee. Wenn Sie zukünftig ein Datum abspeichern, dann können Sie auch dieses gambas-spezifische Datum-Format nehmen. Beachten Sie, dass diese Gleitkommazahlen in Gambas implizit verwendet werden, wenn Operationen mit Datumsangaben durchführt werden.
11.5.2.8.3 UTC und GMT
Die `Koordinierte Weltzeit` UTC (Universal Time Coordinated) ist die Grundlage für die Berechnung von Ortszeiten auf der Welt. Beachten Sie:
- Die Koordinierte Weltzeit (UTC) ist eine Referenzzeit für die Berechnung von Ortszeiten in den verschiedenen Zeitzonen weltweit.
11.5.2.8.4 Programm-Test in einer geänderten Locale
Wenn Sie Ihre Projekte in andere Sprachen übersetzen, dann sollten Sie diese Projekte auch in einer angepassten Test-Umgebung erproben, um mögliche Fehler zu erkennen und zu beseitigen. Über Einträge in den Projekteigenschaften können Sie projekt-bezogen in einer geänderten Locale arbeiten, die auf dem System installiert sein muss. Mit dem Kommando `locale` verschaffen Sie sich zuvor eine Übersicht zur aktuellen Locale auf Ihrem System:
$ locale LANG=de_DE.UTF-8 ... LC_NUMERIC=de_DE.UTF-8 LC_TIME=de_DE.UTF-8 ... LC_IDENTIFICATION=de_DE.UTF-8 LC_ALL=
In der Gambas-IDE verwenden Sie mit ähnlichem Ergebnis den Eintrag Menü> ?> `Systeminformation …`. Dann tragen Sie über Menü> Projekt> Eigenschaften> Umgebung die folgende Umgebungsvariable ein: Variable: LC_ALL mit dem Wert: en_GB.utf8, wenn Sie in einer deutschen Locale arbeiten und in die englische Locale wechseln. Nach dem erfolgreichen Test können Sie die Variable löschen.
Alternativ starten Sie Gambas mit dieser Konfiguration: `$ LC_ALL=en_GB.utf8 gambas3` in der angegebenen Locale. Die Änderung ist nur temporär. An Konfigurationsdateien oder den Projekten wird dadurch nichts dauerhaft geändert. Eine feingranulierte Einstellung zum Beispiel nur für Zahlen und Zeiten erreichen Sie mit: `$ LC_NUMERIC=en_GB.utf8 LC_TIME=en_GB.utf8 gambas3`.
11.5.2.8.5 Arbeit mit Datumsangaben
Der folgende Abschnitt ist eine Ergänzung zu den Kapiteln `9.10 Konvertierungsfunktionen` und `9.3 Datum- und Zeit-Funktionen`. Im Fokus stehen Hinweise zur Arbeit mit Datumsangaben in Bezug auf mögliche Fehlerquellen. Es gilt folgende Festlegung: Wenn vom Datum geschrieben wird, dann ist - je nach Kontext - entweder die vollständige Datumsangabe, der Kalendertag oder nur die Zeitangabe gemeint. Als Datum-Komponenten gelten Sekunde, Minute und Stunde sowie Tag, Monat und Jahr. Arbeiten Sie mit Datumsangaben, dann erfordert das besondere Aufmerksamkeit, wenn neben den Zeitzonen (Locale) – allein für Europa gibt es mehrere – auch noch Zeitumstellungen wie auf Sommerzeit ins Spiel kommen und zu berücksichtigen sind. Um Fehlern vorzubeugen werden anschließend einige Hinweise zur Arbeit mit Datumsangaben gegeben, die danach mit ausgewählten Beispielen belegt werden:
Um eindeutige Datumsangaben zu präsentieren, sollten Sie konkret angeben, welche Zeitzone gemeint ist und deshalb den Offset zu UTC nach der Datumsangabe anfügen oder ein UTC nachstellen (Option). Um Datumsangaben als Zeichenkette auszugeben stehen Ihnen dafür mit Format$() und Str$() Funktionen zur Verfügung, bei den die aktuelle Locale berücksichtigt wird – im Gegensatz zur Funktion CString(). Beim Einsatz der Formatfunktion sollten Sie auch einen Blick auf die Datum- und Zeit-Konstanten unter http://gambaswiki.org/wiki/cat/constant werfen, die vordefinierte Format-Strings verwenden. In der Klasse `Date` der Komponente gb.util finden Sie mehrere Funktionen, mit denen Sie Datumsangaben zum Beispiel von und nach UTC konvertieren können.
Wenn Sie mit der Funktion CDate(Expression AS Variant) eine Zeichenkette oder eine Gleitkommazahl in ein valides Datum konvertieren, so wird davon ausgegangen, dass bei der Datumsangabe keine Locale berücksichtigt wird! Für die Zeichenkette muss das amerikanische Format für eine Datumsangabe verwendet werden: `mM/dD/yyyY hh:mm:ss`, mit dem Monat vor dem Tag. Achtung: Geben Sie Datumsangaben in der Konsole der IDE aus, dann werden diese stets im Format gemäß Locale angezeigt, da die Print-Anweisung intern die Funktion Str$() einsetzt, welche die aktuelle Locale berücksichtigt!
Print CDate("04/10/2019 11:45:30")
Print CDate(2490688.48993056)
Print Date.ToUTC(CDate("04/10/2019 11:45:30")); " (UTC)"
Print Date.ToUTC(CDate(2490688.48993056)); " (UTC)"
> 10.04.2019 13:45:30 > 10.04.2019 13:45:30 > 10.04.2019 11:45:30 (UTC) > 10.04.2019 11:45:30 (UTC)
Um eine lokale Datumsangabe – gegeben in einer Zeichenkette – in ein valides Datum umzuwandeln, sollten Sie die Funktion Val() verwenden und eine Prüfung mit IsDate() voranstellen. Alternativ können Sie die Funktion Date() verwenden, wenn das Datum aus den verschiedenen Komponenten besteht.
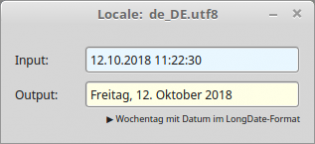
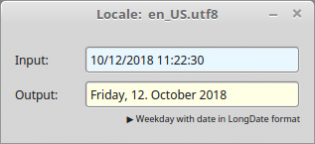
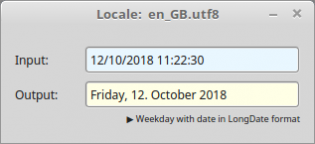
Public Sub TextBox1_Activate() Dim dDate As Date, sMessage As String If Not IsDate(TextBox1.Text) Then sMessage = "<b><font size='+1', color='DarkRed'>Error!</b></font><hr>" sMessage &= "No date - related to the current locale." Message.Error(sMessage) Else dDate = Val(TextBox1.Text) Print "Locale: " & System.Language ' AUSGABEN Print Format$(dDate, gb.ShortDate) Print Format$(dDate, gb.MediumDate) Print Format$(dDate, gb.LongDate) Print Format$(dDate, "dddd, dd. mmmm yyyy") Print Format$(dDate, "dddd, d. mmmm yyyy") TextBox2.Text = Format$(dDate, "dddd, d. mmmm yyyy") Print Format$(dDate, gb.ShortTime) Print Format$(dDate, gb.MediumTime) Print Format$(dDate, gb.LongTime) Print Subst$(("Today is &1, &2 &3, &4"), Format$(dDate, "dddd"), Format$(dDate, "mmmm"), Format$(dDate, "d"), Format$(dDate, "yyyy")) Endif End
Hier werden Ihnen die Ergebnisse präsentiert:
Abbildung 11.5.2.8.4: Ausgabe in Abhängigkeit von der aktuellen Locale
Locale: en_US.utf8 10/12/2018 Oct 12 2018 October Friday 12 2018 Friday, 12. October 2018 Friday, 12. October 2018 11:22 11:22 AM 11:22:30 Today is Friday, October 12, 2018
Abbildung 11.5.2.8.5: Ausgabe in Abhängigkeit von der aktuellen Locale
Locale: en_GB.utf8 12/10/2018 12 Oct 2018 Friday 12 October 2018 Friday, 12. October 2018 Friday, 12. October 2018 11:22 11:22 am 11:22:30 Today is Friday, October 12, 2018
Abbildung 11.5.2.8.6: Ausgabe in Abhängigkeit von der aktuellen Locale
Locale: de_DE.utf8 12.10.2018 12 Okt 2018 Freitag 12 Oktober 2018 Freitag, 12. Oktober 2018 Freitag, 12. Oktober 2018 11:22 11:22 11:22:30 Heute ist Freitag, der 12. Oktober 2018
Eine Besonderheit stellt die Übersetzung in den letzten Zeilen dar, weil die Funktion Subst$() Übersetzungen ermöglicht, die auch die Grammatik berücksichtigen läßt. Der folgende Quelltext-Ausschnitt
Print Subst$(("Today is &1, &2 &3, &4"), Format$(dDate, "dddd"), Format$(dDate, "mmmm"), Format$(dDate, "d"), Format$(dDate, "yyyy"))
wird so im Übersetzungsdialog abgebildet:
Standard: Today is &1, &2 &3, &4 Deutsch (Deutschland): Heute ist &1, der &3. &2 &4